
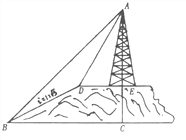
【题目】如图,小山的顶部是一块平地,在这块平地上有一高压输电的铁架,小山的斜坡的坡度![]() ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为![]() ,在山坡的坡顶D处测得铁架顶端A的仰角为
,在山坡的坡顶D处测得铁架顶端A的仰角为![]() ,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
,(1)求小山的高度;(2)求铁架的高度。(结果保留根号)
【答案】小山的高度为25米,铁架的高度为![]() 米.
米.
【解析】试题分析:
试题解析:(1)利用坡度先求出小三高度.(2) 证明△ADE≌△BDF全等,利用勾股定理求铁架的高度.
过D作DF⊥BC,交BC于点F,
∵小山的坡面坡度为1:![]() ,即tan∠DBF=
,即tan∠DBF=![]() ,
,
∴∠DBF=30°,又∠ADE=60°,∠AED=90°,
∴∠DAE=30°,
∵∠CBA=∠CAB=45°,
∴∠CBA-∠DBF=∠CAB-∠DAE,即∠DAB=∠DBA,
∴DB=DA,
在△ADE和△BDF中,
∵∠DAE=∠DBF=30°,∠AED=∠BFD=90°,AD=BD,
∴△ADE≌△BDF(AAS),∴AE=BF,在Rt△BDF中,∠DBF=30°,BD=50米,
∴DF=0.5BD=25米,
根据勾股定理得:BF=![]() 米,则小山的高度为25米,铁架的高度为
米,则小山的高度为25米,铁架的高度为![]() 米.
米.


科目:初中数学 来源: 题型:
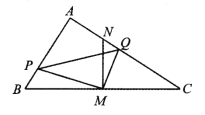
【题目】在△ABC 中,∠BAC=90°,AB<AC,M 是 BC 边的中点,MN⊥BC交 AC 于点 N,动点 P 在线段 BA 上以每秒![]() cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
cm 的速度由点 B 向点 A 运动.同时, 动点 Q 在线段 AC 上由点 N 向点 C 运动,且始终保持 MQ⊥MP. 一个点到终点时,两个点同时停止运动.设运动时间为 t 秒(t>0).
(1)△PBM 与△QNM 相似吗?请说明理由;
(2)若∠ABC=60°,AB=4 ![]() cm.
cm.
①求动点 Q 的运动速度;
②设△APQ 的面积为 s(cm2),求 S 与 t 的函数关系式.(不必写出 t 的取值范围)
(3)探求 BP、PQ、CQ 三者之间的数量关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某市在![]() 天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
天中外出旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 |
|
|
|
|
|
|
|
人数变化(万人) |
|
|
|
|
|
|
|
(1)若![]() 月
月![]() 日外出旅游人数为
日外出旅游人数为![]() ,那么
,那么![]() 月
月![]() 日外出旅游的人数是多少?
日外出旅游的人数是多少?
(2)请判断七天内外出旅游人数最多的是哪天?最少的是哪天?它们相差多少?
(3)如果最多一天有出游人数![]() 万人,那么若
万人,那么若![]() 月
月![]() 日外出旅游的有多少人?
日外出旅游的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
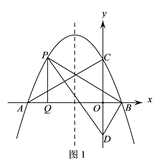
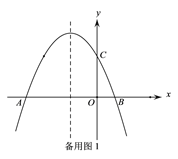
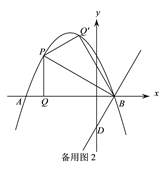
【题目】如图,抛物线y=-![]() x2-
x2-![]() x+
x+![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-
与x轴交于A、B两点(点A在点B的左侧),与y轴于点C,已知点D(0,-![]() ).
).
(1)求直线AC的解析式;
(2)如图1,P为直线AC上方抛物线上的一动点,当△PBD的面积最大时,过P作PQ⊥x轴于点Q,M为抛物线对称轴上的一动点,过M作y轴的垂线,垂足为点N,连接PM、NQ,求PM+MN+NQ的最小值;
(3)在(2)问的条件下,将得到的△PBQ沿PB翻折得到△PBQ′,将△PBQ′沿直线BD平移,记平移中的△PBQ′为△P′B′Q″,在平移过程中,设直线P′B′与x轴交于点E,则是否存在这样的点E,使得△B′EQ″为等腰三角形?若存在,求此时OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图1,⊙O的半径为2, BC是⊙O的弦,点A是⊙O上的一动点。
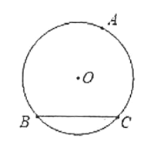
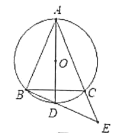
图1 图2
(1)当△ABC的面积最大时,请用尺规作图确定点A位置(尺规作图只保留作图痕迹, 不需要写作法);
(2)如图2,在满足(1)条件下,连接AO并延长交⊙O于点D,连接BD并延长交AC 的延长线于点E,若∠BAC=45° ,求AC2+CE2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校积极响应正在开展的“创文活动”,组织甲、乙两个志愿工程队对所在社区的一些区域进行绿化改造,已知乙工程队每小时能完成的绿化面积是甲工程队每小时能完成的绿化面积的1.5倍,并且乙工程队完成200平方米的绿化面积比甲工程队完成200平方米的绿化面积少用2小时,甲工程队每小时能完成多少平方米的绿化面积?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,点A, 0, B在同一条直线上,OD平分∠AOC, OE平分∠BOC.
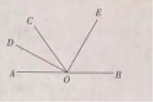
(1)若∠B0D=160°,求∠BOE的度数;
(2) 若∠COE比∠COD多60°.求∠COE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com