
【题目】某商店计划购进甲、乙两种商品,乙种商品的进价是甲种商品进价的九折,用3600元购买乙种商品要比购买甲种商品多买10件.
(1)求甲、乙两种商品的进价各是多少元?
(2)该商店计划购进甲、乙两种商品共80件,且乙种商品的数量不低于甲种商品数量的3倍.甲种商品的售价定为每件80元,乙种商品的售价定为每件70元,若甲、乙两种商品都能卖完,求该商店能获得的最大利润.
【答案】(1)甲、乙两种商品的进价各是40元/件、36元/件;(2)该商店获得的最大利润是2840元.
【解析】
(1)设甲种商品的进价为x元/件,则乙种商品的进价为0.9x元/件,根据题意列出分式方程即可求解;
(2)设甲种商品购进m件,则乙种商品购进(80-m)件,根据题意写出总利润w元,再根据一次函数的图像与性质即可求解.
(1)设甲种商品的进价为x元/件,则乙种商品的进价为0.9x元/件,
![]() ,
,
解得,x=40,
经检验,x=40是原分式方程的解,
∴0.9x=36,
答:甲、乙两种商品的进价各是40元/件、36元/件.
(2)设甲种商品购进m件,则乙种商品购进(80-m)件,总利润为w元,
w=(80-40)m+(70-36)(80-m)=6m+2720,
∵80-m≥3m,
∴m≤20,
∴当m=20时,w取得最大值,此时w=2840,
答:该商店获得的最大利润是2840元.


科目:初中数学 来源: 题型:
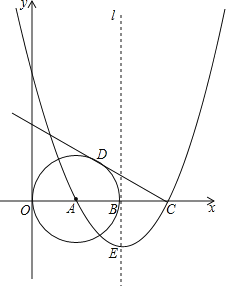
【题目】如图,已知点A(2,0),以A为圆心作⊙A与y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A,抛物线与x轴的另一个交点为点C,抛物线的顶点为点E,如果CO=2BE,求此抛物线的解析式;
(2)过点C作⊙A的切线CD,D为切点,求此切线长;
(3)点F是切线CD上的一个动点,当△BFC与△CAD相似时,求出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,点
是等边三角形,点![]() 是直线
是直线![]() 上一点,以
上一点,以![]() 为一边在
为一边在![]() 的右侧作等边
的右侧作等边![]() .
.
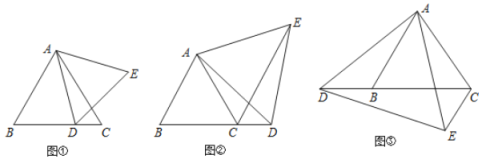
(1)如图①,点![]() 在线段
在线段![]() 上移动时,直接写出
上移动时,直接写出![]() 和
和![]() 的大小关系;
的大小关系;
(2)如图②,点![]() 在线段
在线段![]() 的延长线上移动时,猜想
的延长线上移动时,猜想![]() 的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,交
,交![]() 于点
于点![]() ,在
,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .有以下结论:①
.有以下结论:①![]() 平分
平分![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④
是等边三角形;④![]() ,则正确的结论有( )
,则正确的结论有( )
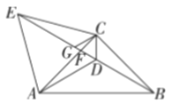
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB是⊙O的切线,切点分别是A、B,直线EF也是⊙O的切线,切点为Q,交PA、PB于点E、F,已知PA=12cm,∠P=40°
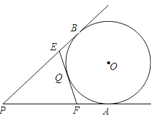
(1)求△PEF的周长.
(2)求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
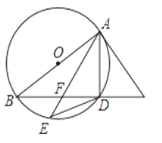
【题目】如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
(1)求证:FD=DC;
(2)若AE=8,DE=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
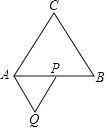
【题目】如图,等边△ABC的边长为6,点P沿△ABC的边从A→B→C运动,以AP为边作等边△APQ,且点Q在直线AB下方,当点P、Q运动到使△BPQ是等腰三角形时,点Q运动路线的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() 是
是![]() 外一点,
外一点,![]() ,
,![]() 分别和
分别和![]() 切于
切于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 上任意一点,过
上任意一点,过![]() 作
作![]() 的切线分别交
的切线分别交![]() ,
,![]() 于
于![]() ,
,![]() .
.

![]() 若
若![]() 的周长为
的周长为![]() ,则
,则![]() 的长为________;
的长为________;
![]() 连接
连接![]() 、
、![]() ,若
,若![]() ,则
,则![]() 的度数为________度.
的度数为________度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com