
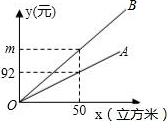
 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
分析 (1)用水单价=用水费÷用水量;
(2)m的值=方案单价×用水量;
(3)现行的、方案一是正比例关系,方案二要分情况计算.
解答 解:(1)现行的用水价为1.84元/立方米,第三阶的用水价格5.22元,故答案为:1.84;5.22;
(2)因为方案一的用水价=1.84+0.96=2.8元/立方米
所以m=2.8×50=140,
设OB的解析式为y=kx,则140=50k,所以k=2.8,
所以y=2.8x;
(3)方案一的情况下:b=2.8a,
方案二的情况下:①当0≤a≤15时,b=2.61a
②当15<a≤25时,b=3.92(a-15)+15×2.61=3.92a-19.65
③当a>25时,b=5.22(a-25)+15×2.61+10×3.92=5.22a-52.15.
点评 此题考查的知识点是一次函数的应用,本题信息量比较大,仔细审题,理清题中各种量的关系十分重要.


科目:初中数学 来源: 题型:填空题
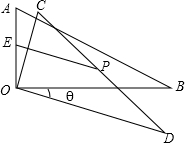 如图,在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△COD.设AO的中点为E,CD中点为P,AO=a,连接EP,当θ=120°时,EP长度最大,最大值为1.5a.
如图,在△AOB中,∠AOB=90°,∠ABO=30°,将△AOB绕顶点O顺时针旋转,旋转角为θ(0°<θ<180°),得到△COD.设AO的中点为E,CD中点为P,AO=a,连接EP,当θ=120°时,EP长度最大,最大值为1.5a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
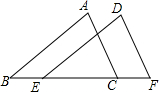 如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )
如图,已知B、E、C、F在同一条直线上,BE=CF,AB∥DE,则下列条件中,不能判断△ABC≌△DEF的是( )| A. | AB=DE | B. | ∠A=∠D | C. | AC∥DF | D. | AC=DF |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com