
����Ŀ����ƽ��ֱ������ϵ�У��ı���AOBC�Ǿ��Σ���O(0��0)����A(5��0)����B(0��3)���Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD��E��F��

(��)��ͼ��������D����BC����ʱ�����D�����ꣻ
(��)��ͼ��������D�����߶�BE��ʱ�� AD��BC���ڵ�H��
����֤��ADB�ա�AOB��
�����H�����꣮
(��)��KΪ����AOBC�Խ��ߵĽ��㣬SΪ��KDE���������S��ȡֵ��Χ(ֱ��д���������)��
���𰸡���I��D(1��3)����II���������������H(![]() ��3)����III��
��3)����III��![]()
��������
(��)��Rt��ACD�����CD���ɽ�����⣻
(��)�ٸ���HL֤�����ɣ�
������֤��BH=AH����AH=BH=m����HC=BC��BH=5��m����Rt��AHC�У�����AH2=HC2+AC2�������������m���ɽ�����⣻
(��)��ͼ���У�����D���߶�BK��ʱ����DEK�������С������D��BA���ӳ�����ʱ����D��E��K������������������Сֵ�Լ����ֵ���ɽ�����⣻
(��)��ͼ���У�
��A(5��0)��B(0��3)��
��OA=5��OB=3��
���ı���AOBC�Ǿ��Σ�
��AC=OB=3��OA=BC=5����OBC=��C=90����
�߾���ADEF���ɾ���AOBC��ת�õ���
��AD=AO=5��
��Rt��ADC��CD=![]() ��
��
��BD=BC��CD=1��
��D(1��3)��
(��)����ͼ���У�����AB��

���ı���ADEF�Ǿ��Σ��õ���ADE=90����
�ߵ�D���߶�BE�ϣ�
���ADB=90����
��AD=AO��AB=AB����AOB=90����
��Rt��ADB��Rt��AOB(HL)��
����ͼ���У��ɡ�ADB�ա�AOB���õ���BAD=��BAO��
�ھ���AOBC�У�OA��BC��
���CBA=��OAB��
���BAD=��CBA��
��BH=AH��
��AH=BH=m����HC=BC��BH=5![]() m��
m��
��Rt��AHC����AH2=HC2+AC2��
��m2=32+(5![]() m)2��
m)2��
��m=![]() ����BH=
����BH=![]() ��
��
��H(![]() ��3)��
��3)��
(��)��ͼ���У�����D���߶�BK��ʱ����DEK�������С��
��Сֵ=![]() DEDK=
DEDK=![]() ��3��(5
��3��(5![]()
![]() )=
)=![]() ��
��

����D��BA���ӳ�����ʱ����D��E��K��������
������=![]() D��E��KD��=
D��E��KD��=![]() ��3��(5+
��3��(5+![]() )=
)=![]() ��
��
����������![]() ��
��


 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д� ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
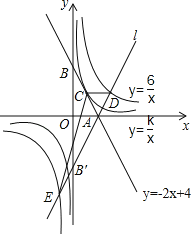
����Ŀ����ͼ��ֱ��y=��2x+4��x���ڵ�A����y���ڵ�B���뷴��������y=![]() ��ͼ����Ψһ�Ĺ�����C��
��ͼ����Ψһ�Ĺ�����C��
��1����k��ֵ��C�����ꣻ
��2��ֱ��l��ֱ��y=��2x+4����x��Գƣ�����y�ύ�ڵ�B'����˫����y=![]() ����D��E���㣬����CDE�������
����D��E���㣬����CDE�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������![]() ��
��![]() ��
��![]() ����ʾ�����ֱ���
����ʾ�����ֱ���![]() ��
��![]() ��3����ش�
��3����ش�
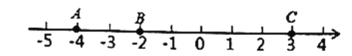
��1����ʹ![]() ��
��![]() ����ľ�����
����ľ�����![]() ��
��![]() ����ľ�����ȣ����轫��
����ľ�����ȣ����轫��![]() �����ƶ�_________����λ���ȣ�
�����ƶ�_________����λ���ȣ�
��2����![]() ��
��![]() ��
��![]() ��ʼ���������˶�������
��ʼ���������˶�������![]() ��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����
��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����![]() �͵�
�͵�![]() �ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶����˶�
�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶����˶�![]() ���Ӻ�
���Ӻ�
����![]() ��
��![]() ��
��![]() ��ʾ�����ֱ���________��________��________���ú�
��ʾ�����ֱ���________��________��________���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
������![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() ����
����![]() ���
���![]() ֮��ľ����ʾΪ
֮��ľ����ʾΪ![]() �����ʣ�
�����ʣ�![]() ��ֵ�Ƿ�����ʱ��
��ֵ�Ƿ�����ʱ��![]() �ı仯���ı䣿���仯����˵�����ɣ������䣬�����
�ı仯���ı䣿���仯����˵�����ɣ������䣬�����![]() ֵ��
ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1���� a �� b �� c �������ϵ�λ����ͼ 1 ��ʾ��| a || c |:

����գ�| a | �� | b a | ��| 2b | ��
�ڻ���| c b | | b a | | a b | ��
�� 2�� a �� b �� c ��С��ϵ��ͼ 2�� ���и�ʽ�� b a (c) 0 �� �� (a) b c 0 ����![]() �� bc a 0 ����| a b | | c b | | a c | 2b ��������ȷ���� ��
�� bc a 0 ����| a b | | c b | | a c | 2b ��������ȷ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�İ뾶Ϊ6��E����O��һ�����㣬��BEΪ�߰�˳ʱ�뷽����������BEDC��M�ǻ�AB���е㣬��E��Բ���ƶ�ʱ��MD����Сֵ��_______
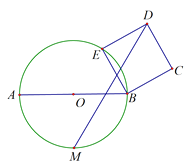
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ���y=��2x+3�����н�����ȷ���ǣ�������
A. ͼ����㣨1����1�� B. ͼ��һ������������
C. y��x����������� D. ��x��![]() ʱ��y��0
ʱ��y��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB��CD������������⣺

��1����ͼ�٣�д����ABE����CDE�͡�E֮���������ϵ���� ����
��2����ͼ�ڣ�BP��DP�ֱ�ƽ�֡�ABE����CDE������E��100�������P�Ķ�����
��3����ͼ�ۣ�����ABP��![]() ��ABE����CDP��
��ABE����CDP��![]() ��CDE����д����P���E��������ϵ����˵�����ɣ�
��CDE����д����P���E��������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
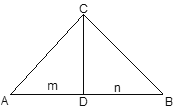
����Ŀ����ͼ,��֪��ABC��,��ACB=90��,��C����CD��AB,����ΪD,��AD=m,BD= n,AC2:BC2=2:1,�ֹ���x�ķ���![]() x2-2(n-1)x+m2-12=0����ʵ�����IJ��ƽ��С��192��
x2-2(n-1)x+m2-12=0����ʵ�����IJ��ƽ��С��192��
��:m��nΪ����ʱ��һ�κ���y=mx+n�Ľ���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC�Ķ���A�ڵ�һ���ޣ���B��C������ֱ�Ϊ��2��1������6��1������BAC=90�㣬AB=AC��ֱ��AB��y���ڵ�P������ABC����A��B��C�����ڵ�P�����ĶԳƣ����A��������Ϊ��������

A. ����4����5�� B. ����5����4�� C. ����3����4�� D. ����4����3��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com