
分析 (1)分子分母同时乘$\sqrt{n+1}-\sqrt{n}$,求解即可,
(2)先化简,再找出规律求解即可.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$(n为正整数)=$\sqrt{n+1}-\sqrt{n}$.
故答案为:$\sqrt{n+1}-\sqrt{n}$.
(2)$\frac{1}{1+\sqrt{2}}$+$\frac{1}{\sqrt{2}+\sqrt{3}}$+$\frac{1}{\sqrt{3}+\sqrt{4}}$+…+$\frac{1}{\sqrt{2013}+\sqrt{2014}}$+$\frac{1}{\sqrt{2014}+\sqrt{2015}}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2015}$-$\sqrt{2014}$,
=$\sqrt{2015}$-1.
点评 本题主要考查了分母有理化,解题的关键是找出式子的规律.


科目:初中数学 来源: 题型:填空题
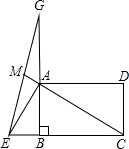 如图,矩形ABCD中,AB=3,AD=3$\sqrt{3}$,点E在CB的延长线上,且BE=$\sqrt{3}$,连结AE,G是BA延长线上一点,连结EG,交CA的延长线于M,将△AEG绕点A逆时针旋转60°得到△AE′G′(点E的对应点为E′,点G的对应点为G′).若△EGG′的面积为6$\sqrt{3}$,则CM的长为7.
如图,矩形ABCD中,AB=3,AD=3$\sqrt{3}$,点E在CB的延长线上,且BE=$\sqrt{3}$,连结AE,G是BA延长线上一点,连结EG,交CA的延长线于M,将△AEG绕点A逆时针旋转60°得到△AE′G′(点E的对应点为E′,点G的对应点为G′).若△EGG′的面积为6$\sqrt{3}$,则CM的长为7.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
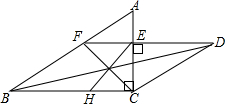 等腰直角△ABC与等腰直角△CDE如图放置,∠ACB=90°,CA=CB,∠CED=90°,EC=ED,点G是BD的中点,连接EG且延长交BC于H,连接CG且延长AB于F,连接EF.
等腰直角△ABC与等腰直角△CDE如图放置,∠ACB=90°,CA=CB,∠CED=90°,EC=ED,点G是BD的中点,连接EG且延长交BC于H,连接CG且延长AB于F,连接EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
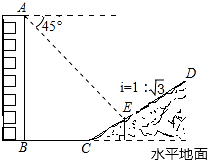 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com