
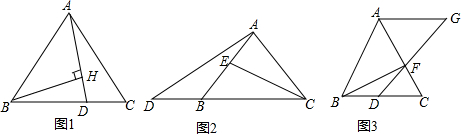
分析 (1)先判断出∠ABD=∠BAD,进而得出△ABE≌△BAH,即可得出BE=AH,代换即可得出结论;
(2)设出AE=x,先利用勾股定理求出BC,进而得出AF,BF,而BD=2,得出DF,再判断出△DAF∽△CEA,得出比例式求出DF即可建立方程,求出x,利用勾股定理即可求出CE;
(3)先判断出三角形ABC是等边三角形,得出∠C=60°,再用三角形的内角和得出∠AFB=∠AFG,进而判断出△AFB≌△AFG,即可得出结论.
解答 解:(1)如图1,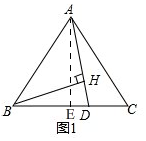
过点A作AE⊥BC于E,
∵AB=AC,
∴BE=$\frac{1}{2}$BC,
∵AD=BD,
∴∠ABD=∠BAD,
在△ABE和△BAH中,$\left\{\begin{array}{l}{∠AEB=∠BHA=90°}\\{∠ABE=∠BAH}\\{AB=BA}\end{array}\right.$,
∴△ABE≌△BAH,
∴BE=AH,
∴$\frac{1}{2}$BC=AH,
∴$\frac{AH}{BC}=\frac{1}{2}$;
(2)如图2,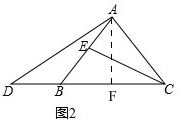
过点A作AF⊥BC于F,设AE=x,
∵点E是AB的中点,
∴AC=AB=2x,
在Rt△ABC中,根据勾股定理得,BC=$\sqrt{2}$AB=2$\sqrt{2}$x,
∴AF=BF=$\frac{1}{2}$BC=$\sqrt{2}$x,
∴DF=BD+BF=2+$\sqrt{2}$x,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°=∠BAF,
∴∠AEC=∠ABC+∠BCE=45°+∠BCE,
∵∠BCE=∠BAD,
∴∠AEC=45°+∠BAD,
∵∠DAF=∠BAF+∠BAD=45°+∠BAD,
∴∠AEC=∠DAF,∵∠AFD=∠EAC=90°,
∴△DAF∽△CEA,
∴$\frac{AF}{AE}$=$\frac{DF}{AC}$,
∴$\frac{\sqrt{2}x}{x}=\frac{DF}{2x}$,
∴DF=2$\sqrt{2}$x,
∵DF=2+$\sqrt{2}$x,
∴2$\sqrt{2}$x=2+$\sqrt{2}$x,
∴x=$\sqrt{2}$,
∴AC=2x=2$\sqrt{2}$,
在Rt△ACE中,根据勾股定理,得CE=$\sqrt{A{E}^{2}+A{C}^{2}}$=$\sqrt{10}$;
(3)∵AB=AC,∠BAC=60°,
∴△ABC是等边三角形,
∴∠C=60°,
在△CDF中,∠CFD=180°-∠CDF-∠C=120°-∠CDF,
∵∠FDC=∠ABF,
∴∠AFG=∠CFD=120°-∠ABF,
在△ABF中,∠AFB=180°-∠BAC-∠ABF=180°-60°-∠ABF=120°-∠ABF,
∴∠AFB=∠AFG,
在△AFB和△AFG中,$\left\{\begin{array}{l}{AF=AF}\\{∠AFB=∠AFG}\\{BF=GF}\end{array}\right.$,
∴△AFB≌△AFG,
∴∠CAG=∠BAC=60°=∠C,
∴AG∥BC.
点评 此题是相似形综合题,主要考查了等腰三角形的三线合一的性质,全等三角形的判定和性质,勾股定理,三角形的内角和,等边三角形的判定和性质,相似三角形的判定和性质,平行线的判定,解(1)的关键是作出辅助线,解(2)的关键是求出AE和AC,解(3)的关键是判断出∠AFB=∠AFG,解本题的难点是作出辅助线构造全等三角形和相似三角形,是一道很好的中考常考题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
 如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
如图,一段抛物线:y=-x(x-3)(0≤x≤3),记为C1,它与x轴交于点O,A1;| A. | ($\frac{69}{2}$,$\frac{9}{4}$) | B. | ($\frac{69}{2}$,-$\frac{9}{4}$) | C. | ($\frac{75}{2}$,$\frac{9}{4}$) | D. | ($\frac{75}{2}$,-$\frac{9}{4}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
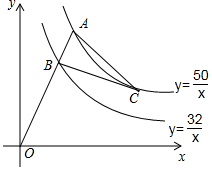 如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )
如图,OA分别与双曲线y=$\frac{50}{x}$(x>0).y=$\frac{32}{x}$(x>0)交于点A,B,BC⊥OA,BC与双曲线y=$\frac{50}{x}$(x>0)交于点C.连结AC,若点B的横坐标为4,则cos∠BAC值为( )| A. | $\frac{\sqrt{10}}{10}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{2\sqrt{3}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{2}{3}$ | B. | m<$\frac{1}{2}$ | C. | m=$\frac{2}{3}$ | D. | m=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为1的正方形网格内有一直角坐标系,其中,A点为(-3,0),B点为(-1,2)
如图,在边长为1的正方形网格内有一直角坐标系,其中,A点为(-3,0),B点为(-1,2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
近年来,我国很多地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数 |
| A | 大气气压低,空气不流动 | m |
| B | 地面灰尘大,空气湿度低 | 20 |
| C | 汽车尾气排放 | n |
| D | 工厂造成的污染 | 80 |
| E | 其他 | 30 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.
如图,已知在△ABC中,AB=AC=10,tan∠B=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分数段 | 频数 | 频率 |
| 72分以下 | 368 | 0.2 |
| 72----80分 | 460 | 0.25 |
| 81----95分 | 644 | 0.35 |
| 96----108分 | 184 | 0.2 |
| 109----119分 | 130 | |
| 120分 | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com