
【题目】(1)问题背景:已知,如图1,等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,AB=a,△ABC的面积为S,则有BC=![]() a,S=
a,S=![]() a2.
a2.
(2)迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②求∠ADB的度数.
③若AD=2,BD=4,求△ABC的面积.
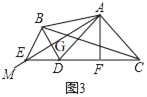
(3)拓展延伸:如图3,在等腰△ABC中,∠BAC=120°,在∠BAC内作射线AM,点D与点B关于射线AM轴对称,连接CD并延长交AM于点E,AF⊥CD于F,连接AD,BE.
①求∠EAF的度数;
②若CD=5,BD=2,求BC的长.

【答案】(1)详见解析;(2)①详见解析;②∠ADB=150°;③5![]() +6.;(3)①∠EAF=60°;②BC=
+6.;(3)①∠EAF=60°;②BC=![]() .
.
【解析】
(1)先判断出∠B=30°,BD=![]() BC,再利用三角函数得出BD=
BC,再利用三角函数得出BD=![]() AB,即可得出结论;
AB,即可得出结论;
(2)①先判断出∠DAB=∠EAC,即可得出结论;
②先判断出∠ADB=∠AEC,再求出∠AEC,即可得出结论;
③先利用勾股定理求出EH,AH,再利用勾股定理求出AC2,借助(1)的结论即可得出结论;
(3)①先判断出∠BAE=∠DAE=![]() ∠BAD,∠DAF=∠CAF=
∠BAD,∠DAF=∠CAF=![]() ∠CAD,即可得出∠EAF=
∠CAD,即可得出∠EAF=![]() ∠BAC=60°,
∠BAC=60°,
②先求出DF=![]() CD=2.5,再判断出△BDE是等边三角形,在Rt△AEF中,求出AE=3
CD=2.5,再判断出△BDE是等边三角形,在Rt△AEF中,求出AE=3![]() ,在Rt△DEG中,EF=
,在Rt△DEG中,EF=![]() ,∴AG=AE﹣EG=2
,∴AG=AE﹣EG=2![]() ,在Rt△ABG中,AB=
,在Rt△ABG中,AB=![]() ,即可得出结论.
,即可得出结论.
解:(1)过点A作AD⊥BC于D,
∵AB=AC,∠BAC=120°,
∴BD=![]() BC,∠BAD=60°,
BC,∠BAD=60°,
∴∠B=30°,cosB=![]() ,
,
∴![]() =
=![]() ,
,
∴BD=![]() AB,
AB,
∴BC=![]() AB=
AB=![]() a.
a.
∴S△ABC=![]() BC×AD=
BC×AD=![]() a2;
a2;
(2)
①∵△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,
∴AD=AE,AB=AC,∠DAB=∠EAC,
在△ADB和△AEC中, ,
,
∴△ADB≌△AEC(SAS),
②由①知,△ADB≌△AEC,
∴∠ADB=∠AEC,
在△ADE中,∠DAE=120°,
∴∠AED=30°,
∴∠AEC=150°,
∴∠ADB=150°,
③如图2,过点A作AH⊥CD于H,
∴DH=EH,
在Rt△ADH中,∠ADE=30°,AD=2,
∴AH=1,
∴DH=EH=![]() ,
,
由①知,△ADB≌△AEC,
∴CE=BD=4,
∴CH=CE+EH=4+![]() ,
,
在Rt△ACH中,AC2=AH2+CH2=20+8![]() ,
,
由(1)得,S△ABC=![]() AC2=
AC2=![]() ×(20+8
×(20+8![]() )=5
)=5![]() +6.
+6.
(3)①∵点B与点D关于AM对称,
∴∠BAE=∠DAE=![]() ∠BAD,AB=AD,
∠BAD,AB=AD,
∵AB=AC,
∴AD=AC,
∵AF⊥CE,
∴∠DAF=∠CAF=![]() ∠CAD,
∠CAD,
∴∠EAF=∠DAE+∠DAF=![]() ∠BAD+
∠BAD+![]() ∠CAD=
∠CAD=![]() (∠BAD+∠CAD)=
(∠BAD+∠CAD)=![]() ∠BAC=60°,
∠BAC=60°,
②∵CD=5,
∴DF=![]() CD=2.5,
CD=2.5,
由①知,∠AEF=90°﹣∠EAF=30°,
由对称得,BG=DG=![]() BD=1,∠BED=2∠AEF=60°,BE=DE,
BD=1,∠BED=2∠AEF=60°,BE=DE,
∴△BDE是等边三角形,
∴DE=BD=2,
∴EF=4.5,
在Rt△AEF中,cos∠AEF=![]() ,
,
∴cos30°=![]() ,
,
∴AE=3![]() ,
,
在Rt△DEG中,EF=![]() ,
,
∴AG=AE﹣EG=2![]() ,
,
在Rt△ABG中,AB=![]() =
=![]() ,
,
由(1)知,BC=![]() AB=
AB=![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,以下哪辆车可以通过?( )
(栏杆宽度,汽车反光镜忽略不计)
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)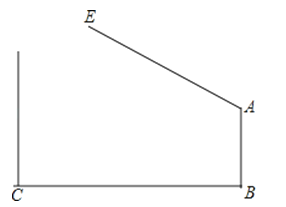
A.宝马Z4(4200mm×1800mm×1360mm)
B.奇瑞QQ(4000mm×1600mm×1520mm)
C.大众朗逸(4600mm×1700mm×1400mm)
D.奥迪A4(4700mm×1800mm×1400mm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边上的一点,∠B=44°,∠BAD=28°,将△ABD沿AD折叠得到△AED,AE与BC交于点F.
(1)填空:∠AFC= 度;
(2)求∠EDF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论: ①4ac﹣b2<0;②4a+c<2b;③3b+2c<0;④m(am+b)+b<a(m≠﹣1),
其中正确结论的个数是( )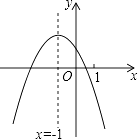
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 经过原点和点
经过原点和点![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求直线![]() 所对应的函数解析式;
所对应的函数解析式;
(2)当P在线段OA上时,设![]() 点横坐标为
点横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,写出
,写出![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(3)当P在射线OA上时,在坐标轴上有一点![]() ,使
,使![]() (
(![]() 正整数),请直接写出点
正整数),请直接写出点![]() 的坐标(本小题只要写出结果,不需要写出解题过程)
的坐标(本小题只要写出结果,不需要写出解题过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴的一个交点为A(3,0),与y轴的交点为B(0,3),其顶点为C,对称轴为x=1.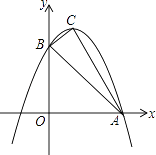
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ABM为等腰三角形时,求点M的坐标;
(3)将△AOB沿x轴向右平移m个单位长度(0<m<3)得到另一个三角形,将所得的三角形与△ABC重叠部分的面积记为S,用m的代数式表示S.
查看答案和解析>>
科目:初中数学 来源: 题型:
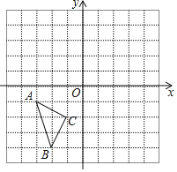
【题目】在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(–3,–1).
(1)将△ABC先沿x轴向右平移3个单位,再沿y轴向上平移2个单位得到△A1B1C1,画出△A1B1C1,并写出点B1坐标.
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
(3)求出△A2B2C2的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com