
已知一个正n边形的外接圆半径和内切圆半径分别为20 mm、10![]() mm,求这个多边形的边长和面积.
mm,求这个多边形的边长和面积.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
图1所示的遮阳伞,伞的外边缘是一个正八边形,伞炳垂直于水平地面,起示意图如图2.当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开.已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米.
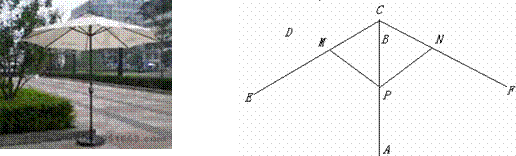

(1)当∠CPN=60度时,求AP的长度;
(2)设阳光直射下伞的阴影(正八边形)面积的最大值.(精确到0.1分米)参考数据![]() 1)
1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com