
【题目】如图①,直角三角形ABC中,∠B=90°.将它放在平面直角坐标系中,A(0,1),且满足(AB-4)2+![]() =0.
=0.
(1)求直线AC的解析式.
(2)在直线BC上是否存在点P,使S△APC= 6?若存在,求P点坐标;若不存在,说明理由.
(3)如果M在y轴上,且△AMC是以AC为腰的等腰三角形,求M的坐标
(4)如果D是AC的中点,问在y轴上是否存在点M,使得MD+ ![]() AC最小?存在的话,请直接写出M的坐标。
AC最小?存在的话,请直接写出M的坐标。

 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】选取二次三项式![]() 中的两项,配成完全平方式的过程叫做配方.例如
中的两项,配成完全平方式的过程叫做配方.例如
①选取二次项和一次项配方:![]() ;
;
②选取二次项和常数项配方:![]() ,或
,或![]() ;
;
③选取一次项和常数项配方:![]() .
.
根据上述材料,解决下面问题:
![]() 写出
写出![]() 的两种不同形式的配方;
的两种不同形式的配方;
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若关于
若关于![]() 的代数式
的代数式![]() 是完全平方式,求
是完全平方式,求![]() 的值;
的值;
![]() 用配方法证明:无论
用配方法证明:无论![]() 取什么实数时,总有
取什么实数时,总有![]() 恒成立.
恒成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB=2,BC=1,CD=2,AD=3,连接AC.
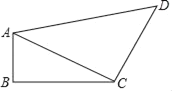
(1)求AC的长;
(2)判断三角形ACD的形状,并求出四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发1小时后到达南亚所(景点),游玩一段时间后按原速前往湖光岩.小明离家1小时50分钟,妈妈驾车沿相同路线前往湖光岩,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.

(1)求小明骑车的速度和在南亚所游玩的时间;
(2)若妈妈在出发后25分钟时,刚好在湖光岩门口追上小明,求妈妈驾车的速度及CD所在直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市创建“绿色发展模范城市”,针对境内长江段两种主要污染源:生活污水和沿江工厂污染物排放,分别用“生活污水集中处理”(下称甲方案)和“沿江工厂转型升级”(下称乙方案)进行治理,若江水污染指数记为Q,沿江工厂用乙方案进行一次性治理(当年完工),从当年开始,所治理的每家工厂一年降低的Q值都以平均值n计算.第一年有40家工厂用乙方案治理,共使Q值降低了12.经过三年治理,境内长江水质明显改善.
(1)求n的值;
(2)从第二年起,每年用乙方案新治理的工厂数量比上一年都增加相同的百分数m,三年来用乙方案治理的工厂数量共190家,求m的值,并计算第二年用乙方案新治理的工厂数量;
(3)该市生活污水用甲方案治理,从第二年起,每年因此降低的Q值比上一年都增加个相同的数值a.在(2)的情况下,第二年,用乙方案所治理的工厂合计降低的Q值与当年因甲方案治理降低的Q值相等,第三年,用甲方案使Q值降低了39.5.求第一年用甲方案治理降低的Q值及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上1、2、3、4四个数字;转盘B被均匀地分成6等份,每份分别标上1、2、3、4、5、6六个数字。有人为甲、乙两人设计了一个游戏,其规则如下:
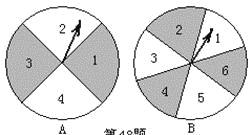
同时自由转动转盘A与B转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针停留在某一数字为止),用所指的两个数字作乘积,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,那么乙胜(如转盘A指针指向3,转盘B指针指向5,3×5=15,按规则乙胜)。你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的一元二次方程
的一元二次方程![]() .
.
![]() 若方程有实数根,求
若方程有实数根,求![]() 的取值范围;
的取值范围;
![]() 如果
如果![]() 是满足条件的最大的整数,且方程
是满足条件的最大的整数,且方程![]() 一根的相反数是一元二次方程
一根的相反数是一元二次方程![]() 的一个根,求
的一个根,求![]() 的值及这个方程的另一根.
的值及这个方程的另一根.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com