
过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为( )
A. 3cm B. 6cm C.  cm D. 9cm
cm D. 9cm
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:单选题
已知2m+3n=5,则4m·8n=( )
A. 16 B. 25 C. 32 D. 64
C 【解析】∵, ∴. 故选C.查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
如图,一圆柱高8 cm,底面半径为 cm,一只蚂蚁从点
cm,一只蚂蚁从点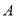 爬到点
爬到点 处吃食,要爬行的最短路程是( )cm.
处吃食,要爬行的最短路程是( )cm.

A. 6 B. 8 C. 10 D. 12
C 【解析】【解析】 底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为: ×2π×=6(cm),展开后的图形中,有BC=8cm,AC=6cm,根据勾股定理得:AB==10(cm).故选C.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC= ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).
,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).

查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:单选题
在平面直角坐标系中,△ABC顶点A的坐标为(2,3).若以原点O为位似中心,画△ABC的位似图形△A′B′C′,使△ABC与△A′B′C′的相似比为 ,则点A′的坐标为( )
,则点A′的坐标为( )
A. (3,  ) B. (3,
) B. (3, 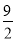 )或(-3,
)或(-3,  )
)
C. ( ,-2) D. (
,-2) D. ( ,2)或(
,2)或(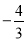 ,-2)
,-2)
查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:解答题
如图,线段AB=60厘米.
(1)点P沿线段AB自A点向B点以4厘米/分的速度运动,同时点Q沿线段自B点向A点以6厘米/分的速度运动,几分钟后,P、Q两点相遇?
(2)几分钟后,P、Q两点相距20厘米?

查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:填空题
一个两位数,个位数字是十位数字的4倍,如果把个位数字与十位数字对调,那么得到的新数比原数大54,则原数为________.
28 【解析】【解析】 设原数十位数字为x,则个位数字为4x,根据题意可得: 40x+x﹣(10x+4x)=54,解得:x=2,故4x=8. 故原数为28.故答案为:28.查看答案和解析>>
科目:初中数学 来源:山西省吕梁市孝义市2016-2017学年九年级(上)期末考试数学试卷 题型:解答题
为了响应国家“自主创业”的号召,某大学毕业生开办了一个装饰品商店,采购了一种今年刚上市的饰品进行了30天的试销,购进价格为20元/件,销售结束后,得知日销售量P(件)与销售时间x(天)之间的关系如图(1)所示,销售价格Q(元/件)与销售时间x(天)之间的关系如图(2)所示.

(1)根据图象直接写出:日销售量P(件)与销售时间x(天)之间的函数关系式为 ;销售单价
Q(元/件)与销售时间x(天)的函数关系式为 .(不要求写出自变量的取值范围)
(2)写出该商品的日销售利润W(元)和销售时间x(天)之间的函数关系式;(不要求写出自变量的取值范围)
(3)请问在30天的试销售中,哪一天的日销售利润最大?并求出这个最大利润.
(1)P=﹣2x+80,Q=x+30;(2)W=﹣x2+20x+800;(3)在30天的试销中,第10天的日销售利润最大,最大利润为900元 【解析】试题分析:(1)设P=kx+80,将(30,20)代入可求出k的值,得出日销售量P(件)与销售时间x(天)之间的函数关系式;设Q=mx+30,将(30,45)代入可求出m的值,得出Q(元/件)与销售时间x(天)的函数关系式; (2)根据销...查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省大庆市杜尔伯特县九年级(上)期末数学试卷(五四学制) 题型:单选题
把抛物线y=﹣2x2向上平移1个单位,再向右平移1个单位,得到的抛物线是( )
A. y=﹣2(x+1)2+1 B. y=﹣2(x﹣1)2+1 C. y=﹣2(x﹣1)2﹣1 D. y=﹣2(x+1)2﹣1
B 【解析】试题解析:∵函数y=-2x2的顶点为(0,0), ∴向上平移1个单位,再向右平移1个单位的顶点为(1,1), ∴将函数y=-2x2的图象向上平移1个单位,再向右平移1个单位,得到抛物线的解析式为y=-2(x-1)2+1, 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com