
【题目】如图,在四边形![]() 中,
中,![]() ,连接
,连接![]() ,
,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,则图中的全等三角形共有( )
,则图中的全等三角形共有( )

A.4对B.3对C.2对D.1对
【答案】B
【解析】
先利用AAS证△ABF≌△CDE,利用全等性质得出AF=EC,推出AE=FC,再利用SAS证△ADE≌△CBF,利用SSS证△ABC≌△CDA,.
解:∵在四边形![]() 中,
中,![]()
∴四边形![]() 是平行四边形
是平行四边形
∴AB=CD
∠BAF=∠ECD
∵![]()
∴∠DEF=∠BFE
∴在△ABF与△CDE
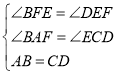
∴△ABF≌△CDE(AAS)
∴AF=EC,AB=CD
∴AF-EF=EC-EF即AE=FC
∵![]()
∴∠DAE=∠FCB
∴在△ADE与△CBF
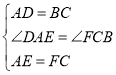
则△ADE≌△CBF(SAS)
在△ABC与△CDA
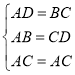
∴△ABC≌△CDA(SSS)
图中全等三角形有△ABF≌△CDE, △ADE≌△CBF, △ABC≌△CDA,共3对.
故选:B.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】尺规作图(不要求写出作法,请保留作图痕迹):

(1)如图1,经过已知直线![]() 外一点
外一点![]() 作这条直线的垂线;
作这条直线的垂线;
(2)如图2,已知等腰三角形底边长为![]() ,底边上的高为
,底边上的高为![]() ,求作这个等腰三角形.
,求作这个等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两次收购某时令蔬菜200吨,第一批蔬菜价格为2000元/吨,因蔬菜大量上市,第二批收购时价格变为500元/吨,这两批蔬菜共用去16万元.
(1)求两批次购蔬菜各购进多少吨?
(2)公司收购后对蔬菜进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润800元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个正整数![]() 能表示成
能表示成![]() (
(![]() 是正整数,且
是正整数,且![]() )的形式,则称这个数为“明礼崇德数”,
)的形式,则称这个数为“明礼崇德数”,![]() 与
与![]() 是
是![]() 的一个平方差分解. 例如:因为
的一个平方差分解. 例如:因为![]() ,所以5是“明礼崇德数”,3与2是5的平方差分解;再如:
,所以5是“明礼崇德数”,3与2是5的平方差分解;再如:![]() (
(![]() 是正整数),所以
是正整数),所以![]() 也是“明礼崇德数”,
也是“明礼崇德数”,![]() 与
与![]() 是
是![]() 的一个平方差分解.
的一个平方差分解.
(1)判断:9_______“明礼崇德数”(填“是”或“不是”);
(2)已知![]() (
(![]() 是正整数,
是正整数,![]() 是常数,且
是常数,且![]() ),要使
),要使![]() 是“明礼崇德数”,试求出符合条件的一个
是“明礼崇德数”,试求出符合条件的一个![]() 值,并说明理由;
值,并说明理由;
(3)对于一个三位数,如果满足十位数字是7,且个位数字比百位数字大7,称这个三位数为“七喜数”.若![]() 既是“七喜数”,又是“明礼崇德数”,请求出
既是“七喜数”,又是“明礼崇德数”,请求出![]() 的所有平方差分解.
的所有平方差分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
已知:如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() 是
是![]() 平分线,交
平分线,交![]() 边于点
边于点![]() .
.

求证:![]() .
.
证明:在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
则由已知条件易知:![]() .
.
∴![]() ,
,
又∵![]() ,∴
,∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ∴
∴![]() .
.
(数学思考)
现将原题中的“![]() 是
是![]() 平分线,交
平分线,交![]() 边于点
边于点![]() ”换成“
”换成“![]() 是
是![]() 的外角平分线,交
的外角平分线,交![]() 边的延长线于点
边的延长线于点![]() ”,如图,其他条件不变,请你猜想线段
”,如图,其他条件不变,请你猜想线段![]() 之间的数量关系,并证明你的猜想.
之间的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为响应市政府“绿色出行”的号召,小张上班由自驾车改为骑公共自行车.已知小张家距上班地点10千米.他用骑公共自行车的方式平均每小时行驶的路程比他用自驾车的方式平均每小时行驶的路程少45千米,他从家出发到上班地点,骑公共自行车方式所用的时间是自驾车方式所用的时间的4倍.小张用骑公共自行车方式上班平均每小时行驶多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C,AB=16cm,BC=12cm,D为AB的中点.若点P在线段BC上以4cm/s的速度由B向C运动,同时,点Q在线段CA上以a(cm/s)的速度由C向A运动,设运动的时间为t(s)(0≤t≤3)

(1)用关于t的代数式表示PC的长度.
(2)若点P,Q的运动速度相等,经过1s后,△BPD与△CQP是否全等?请说明理由.
(3)若点PQ的运动速度不相等,当点Q的运动速度a为多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com