
【题目】如图,在![]() 中,点D、E分别是边BC、AC的中点,过点A作
中,点D、E分别是边BC、AC的中点,过点A作![]() 交DE的延长线于F点,连接AD、CF.
交DE的延长线于F点,连接AD、CF.
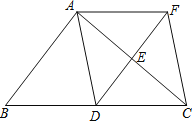
(1)求证:四边形ADCF是平行四边形;
(2)当![]() 满足什么条件时,四边形图ADCF是菱形?为什么?
满足什么条件时,四边形图ADCF是菱形?为什么?
【答案】(1)见解析;(2)当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,理由见解析.
【解析】
(1)首先利用平行四边形的判定方法得出四边形ABDF是平行四边形,进而得出AF=DC,利用一组对边相等且平行的四边形是平行四边形,进而得出答案;
(2)利用直角三角形的性质结合菱形的判定方法得出即可.
(1)证明:∵点D、E分别是边BC、AC的中点,
∴DE∥AB,BD=CD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∴AF=BD,则AF=DC,
∵AF∥BC,
∴四边形ADCF是平行四边形;
(2)解:当△ABC是直角三角形,且∠BAC=90°时,四边形ADCF是菱形,
理由:∵△ABC是直角三角形,且∠BAC=90°
又∵点D是边BC的中点,
∴AD=DC,
∴平行四边形ADCF是菱形.


科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,E为AB边上一点,∠BCE=16°,EF∥BC交DC于点F.
(1)依题意补全图形,并求∠FEC的度数;
(2)若∠A=141°,求∠AEC的度数.
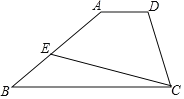
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如 1, 0 ,2, 0 , 2,1 , 3,1 , 3, 0 ……根据这个规律探索可得,第 2019 个点的坐标为
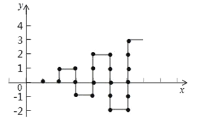
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面文字,然后按要求解题.
例:1+2+3+…+100=?如果一个一个顺次相加显然太麻烦,我们仔细分析这100个连续自然数的规律和特点,可以发现运用加法的运算律,是可以大大简化计算,提高计算速度的.因为1+100=2+99=3+98=…=50+51=101,所以将所给算式中各加数经过交换、结合以后,可以很快求出结果:
1+2+3+4+5+…+100
=(1+100)+(2+99)+(3+98)+…+(50+51)
=101× = .
(1)补全例题解题过程;
(2)请猜想:1+2+3+4+5+6+…+(2n﹣2)+(2n﹣1)+2n= .
(3)试计算:a+(a+b)+(a+2b)+(a+3b)+…+(a+99b).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你能化简(m﹣1)(m99+m98+…+m+1)吗?遇到这样的复杂问题时,我们可以先从简单的情形入手,探究归纳出一些方法.
(1)分别化简下列各式:
(m﹣1)(m+1)=m2﹣1;
(m﹣1)(m2+m+1)= ;
(m﹣1)(m3+m2+m+1)= ;
(m﹣1)(mn+mn﹣1+mn﹣2+…+m+1)= .
(2)请你利用上面的结论计算:299+298+297+…+2+1,写出计算过程.
(3)根据以上计算经验,直接写出3n+3n﹣1+3n﹣2+…+3+1结果 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们在学习《从面积到乘法公式》时,曾用两种不同的方法计算同一个图形的面积,探索了单项式乘多项式的运算法则:m(a+b+c)=ma+mb+mc(如图1),多项式乘多项式的运算法则:
(a+b)(c+d)=ac+ad+bc+bd(如图2),以及完全平方公式:(a+b)2=a2+2ab+b2(如图3).
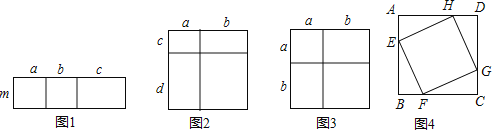
把几个图形拼成一个新的图形,通过图形面积的计算,常常可以得到一些等式,这是研究数学问题的一种常用方法.
(1)请设计两个图形说明一下两个等式成立(画出示意图,并标上字母)
①(a+b)(2a+b)=2a2+3ab+b2
②(a+b+c)2=a2+b2+c2+2ab+2ac+2bc
(2)如图4,它是由四个形状、大小完全相同的直角三角形与中间的小正方形EFGH拼成的一个大正方形ABCD.如果每个直角三角形的较短的边长为a,较长的边长为b,最长的边长为c.试用两种不同的方法计算这个大正方形的面积,你能发现直角三角形的三边长a、b、c的什么数量关系?(注:写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F.若BF=12,AB=10,则AE的长为( )

A. 10 B. 12 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4~7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型, A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2),请回答下列问题:
(1)在这次调查中D类型有多少名学生?
(2)写出被调查学生每人植树量的众数、中位数;
(3)求被调查学生每人植树量的平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
(1)如图①,边长为4的等边△OAB位于平面直角坐标系中,将△OAB折叠,使点B落在OA的中点处,则折痕长为 ;
(2)如图②,矩形OABC位于平面直角坐标系中,其中OA=8,AB=6,将矩形沿线段MN折叠,点B落在x轴上,其中AN=![]() AB,求折痕MN的长;
AB,求折痕MN的长;
问题解决:
(3)如图③,四边形OABC位于平面直角坐标系中,其中OA=AB=6,CB=4,BC∥OA,AB⊥OA于点A,点Q(4,3)为四边形内部一点,将四边形折叠,使点B落在x轴上,问是否存在过点Q的折痕,若存在,求出折痕长,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com