
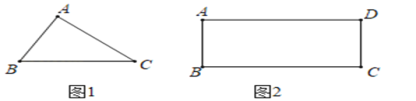
【题目】(1)如图1,已知△ABC,试确定一点D,使得以A,B,C,D为顶点的四边形为平行四边形,请画出这个平行四边形;
(2)如图2,在矩形ABCD中,AB=4,BC=10,若要在该矩形中作出一个面积最大的△BPC,且使∠BPC=90°,求满足条件的点P到点A的距离;
【答案】(1)详见解析;(2)2或8
【解析】
(1)利用平行四边形的判定方法画出图形即可.
(2)以点O为圆心,OB长为半径作⊙O,⊙O一定于AD相交于P1,P2两点,点P1,P2即为所求.
解:(1)如图记为点D所在的位置.
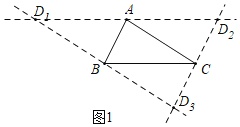
(2)如图,
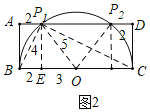
∵AB=4,BC=10,∴取BC的中点O,则OB>AB.
∴以点O为圆心,OB长为半径作⊙O,⊙O一定于AD相交于P1,P2两点,
连接BP1,P1C,P1O,∵∠BPC=90°,点P不能再矩形外;
∴△BPC的顶点P1或P2位置时,△BPC的面积最大,
作P1E⊥BC,垂足为E,则OE=3,
∴AP1=BE=OB﹣OE=5﹣3=2,
由对称性得AP2=8.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
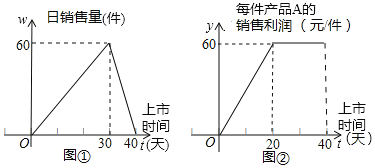
【题目】某商场销售产品A,第一批产品A上市40天内全部售完.该商场对第一批产品A上市后的销售情况进行了跟踪调查,调查结果如图所示:图①中的折线表示日销售量w与上市时间t的关系;图②中的折线表示每件产品A的销售利润y与上市时间t的关系.
(1)观察图①,试写出第一批产品A的日销售量w与上市时间t的关系;
(2)第一批产品A上市后,哪一天这家商店日销售利润Q最大?日销售利润Q最大是多少元?(日销售利润=每件产品A的销售利润×日销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某市对位于笔直公路AC上两个小区A,B的供水路线进行优化改造,供水站M在笔直公路AD上,测得供水站M在小区A的南偏东60°方向,在小区B的西南方向,小区A,B之间的距离为300(![]() +1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)
+1)米,求供水站M分别到小区A,B的距离.(结果可保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC,PF⊥CD,垂足分别为点E,F,连接AP,EF,给出下列四个结论:

①AP=EF;②∠PFE=∠BAP;③PD=![]() EC;④△APD一定是等腰三角形.
EC;④△APD一定是等腰三角形.
其中正确的结论有( ).
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
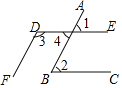
【题目】如图,∠1=60°,∠2=60°,∠3=120°.
试说明DE∥BC,DF∥AB,根据图形,完成下列推理:
∵∠1=60°,∠2=60°(已知)
∴∠1=∠2(等量代换)
∴ ∥ ( )
∵AB,DE相交,
∴∠4=∠1=60°
∵∠3=120°
∴∠3+∠4=180°
∴ ∥ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A′________;B′________;C′________;
(2)说明△A′B′C′由△ABC经过怎样的平移得到;
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为________;
(4)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,边长为![]() 的等边
的等边![]() 的项点
的项点![]() 都在
都在![]() 轴上,顶点
轴上,顶点![]() 在第二象限内,
在第二象限内,![]() 经过平移或轴对称或旋转都可以得到
经过平移或轴对称或旋转都可以得到![]() .
.
(1)![]() 沿
沿![]() 轴向右平移得到
轴向右平移得到![]() ,则平移的距离是 个长度单位;
,则平移的距离是 个长度单位;![]() 与
与![]() 关于直线对称,则对称轴是 ,
关于直线对称,则对称轴是 ,![]() 绕原点
绕原点![]() 顺时针方向旋转得到
顺时针方向旋转得到![]() ,则旋转角度至少是 度;
,则旋转角度至少是 度;
(2)连接![]() ,交
,交![]() 于点
于点![]() ,求
,求![]() 的度数.
的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小东根据学习一次函数的经验,对函数y=|2x﹣1|的图象和性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=|2x﹣1|的自变量x的取值范围是 ;
(2)已知:
①当x=![]() 时,y=|2x﹣1|=0;
时,y=|2x﹣1|=0;
②当x>![]() 时,y=|2x﹣1|=2x﹣1
时,y=|2x﹣1|=2x﹣1
③当x<![]() 时,y=|2x﹣1|=1﹣2x;
时,y=|2x﹣1|=1﹣2x;
显然,②和③均为某个一次函数的一部分.
(3)由(2)的分析,取5个点可画出此函数的图象,请你帮小东确定下表中第5个点的坐标(m,n),其中m= ;n= ;:
x | … | ﹣2 | 0 |
| 1 | m | … |
y | … | 5 | 1 | 0 | 1 | n | … |
(4)在平面直角坐标系xOy中,作出函数y=|2x﹣1|的图象;
(5)根据函数的图象,写出函数y=|2x﹣1|的一条性质.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com