
(1)观察发现
如图(1):若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
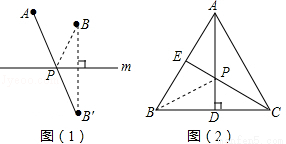
如图(2):在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 .
(2)实践运用
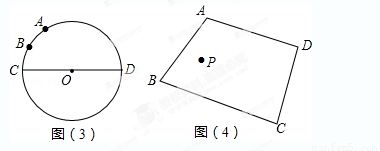
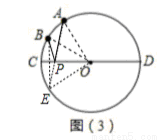
如图(3):已知⊙O的直径CD为2, 的度数为60°,点B是
的度数为60°,点B是 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,求BP+AP的最小值.
的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,求BP+AP的最小值.
(3)拓展延伸
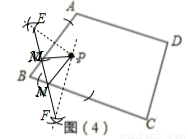
如图(4):点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使△PMN的周长最小,保留作图痕迹,不写作法.
(1) 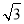 ;(2)
;(2) 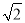 ;(3)作图见解析.
;(3)作图见解析.
【解析】
试题分析:(1)观察发现:利用作法得到CE的长为BP+PE的最小值;由AB=2,点E是AB的中点,根据等边三角形的性质得到CE⊥AB,∠BCE=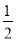 ∠BCA=30°,BE=1,再根据含30度的直角三角形三边的关系得CE=
∠BCA=30°,BE=1,再根据含30度的直角三角形三边的关系得CE=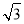 ;
;
(2)实践运用:过B点作弦BE⊥CD,连结AE交CD于P点,连结OB、OE、OA、PB,根据垂径定理得到CD平分BE,即点E与点B关于CD对称,则AE的长就是BP+AP的最小值;由于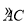 的度数为60°,点B是
的度数为60°,点B是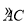 的中点得到∠BOC=30°,∠AOC=60°,所以∠AOE=60°+30°=90°,于是可判断△OAE为等腰直角三角形,则AE=
的中点得到∠BOC=30°,∠AOC=60°,所以∠AOE=60°+30°=90°,于是可判断△OAE为等腰直角三角形,则AE=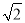 OA=
OA=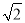 ;
;
(3)拓展延伸:分别作出点P关于AB和BC的对称点E和F,然后连结EF,EF交AB于M、交BC于N.
试题解析:(1)观察发现
如图(2),CE的长为BP+PE的最小值,
∵在等边三角形ABC中,AB=2,点E是AB的中点
∴CE⊥AB,∠BCE=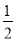 ∠BCA=30°,BE=1,
∠BCA=30°,BE=1,
∴CE=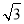 BE=
BE=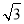 ;
;
(2)实践运用
如图(3),过B点作弦BE⊥CD,连结AE交CD于P点,连结OB、OE、OA、PB,
∵BE⊥CD,
∴CD平分BE,即点E与点B关于CD对称,
∵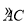 的度数为60°,点B是
的度数为60°,点B是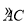 的中点,
的中点,
∴∠BOC=30°,∠AOC=60°,
∴∠EOC=30°,
∴∠AOE=60°+30°=90°,
∵OA=OE=1,
∴AE=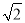 OA=
OA=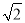 ,
,
∵AE的长就是BP+AP的最小值.
故答案为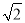 ;
;
(3)拓展延伸:如图(4).
考点:1.圆的综合题;2.轴对称-最短路线问题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:2014-2015学年湖南省株洲市攸县七年级上学期期末测试数学试卷(解析版) 题型:解答题
(本题满分8分,每小题4分)解方程:
(1)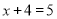
(2)已知方程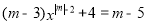 是关于x 的一元一次方程.求m的值并解这个一元一次方程.
是关于x 的一元一次方程.求m的值并解这个一元一次方程.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知关于x 的一元二次方程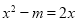 有两个不相等的实数根,则m的取值范围是( )
有两个不相等的实数根,则m的取值范围是( )
A.m>-1 B.m<-2 C.m ≥0 D.m<0
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图所示,给出下列条件:①∠B?∠ACD;②∠ADC?∠ACB;③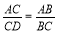 ;④AC2?AD·AB.其中单独能够判定△ABC∽△ACD的个数为( )
;④AC2?AD·AB.其中单独能够判定△ABC∽△ACD的个数为( )
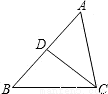
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级上学期期末考试数学试卷(解析版) 题型:选择题
下列四个图形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )
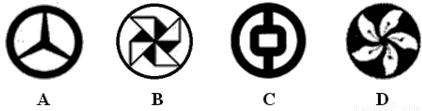
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:解答题
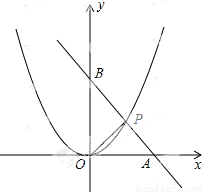
已知,如图,直线l经过A(4,0)和B(0,4)两点,它与抛物线y=ax2在第一象限内相交于点P,又知△AOP的面积为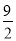 ,求抛物线的函数表达式.
,求抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级上学期第二次质量抽测数学试卷(解析版) 题型:填空题
已知x=1是一元二次方程x2+kx-2=0的一根,则方程的另一个根为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省宜兴市九年级11月阶段性检测数学试卷(解析版) 题型:解答题
已知如图1,Rt△ABC和Rt△ADE的直角边AC和AE重叠在一起,AD=AE,∠B=30°,∠DAE=∠ACB=90°.

(1)如图1,填空:∠BAD= ;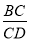 = ;
= ;
(2)如图2,将△ADE绕点A顺时针旋转,使AE到AB边上,∠ACH=∠BCH,连接BH,求∠CBH的度数;
(3)如图3,点P是BE上一点,过A、E两点分别作AN⊥PC、EM⊥PC,垂足分别为N、M,若EM=2,AN=5,求△AND的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市宝应县九年级上学期期末测试数学试卷(解析版) 题型:填空题
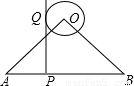
如图,Rt△AOB中,∠O=90°,OA=OB=3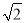 ,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为
,⊙O的半径为1,P是AB边上的动点,过点P作⊙O的切线PQ,切点为Q,则切线长PQ的最小值为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com