
【题目】如图,矩形ABCD中,AB=3,BC=5,点E是AD边上一点,BE=BC.
(1)求证:EC平分∠BED.
(2)过点C作CF⊥BE,垂足为点F,连接FD,与EC交于点O,求FD·EC的值.
【答案】
(1)证明:作CF垂直BE于F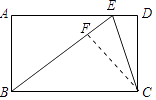
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEC=∠BCE,
∵BE=BC,
∴∠BEC=∠BCE,
∴∠DEC=∠BEC,
即EC平分∠BED.
(2)解:如图所示: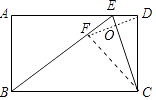
∵CF⊥EB,CD⊥ED,EC平分∠BED,
∴CF=CD=3,
在Rt△ABE中,∵AB=3,BE=BC=5,
∴AE= ![]() =4,
=4,
∴DE=1,
在Rt△ECD和Rt△ECF中,![]() ,
,
∴Rt△ECD≌Rt△ECF,
∴ED=EF=1,∵CF=CD=3,
∴EC垂直平分线段DF,
∴S四边形EFCD=2S△EDC= ![]() ECDF,
ECDF,
∴ ![]() ECDF=2×
ECDF=2× ![]() ×3×1=3,
×3×1=3,
∴ECDF=6.
【解析】(1)根据已知BE=BC,可证出∠BEC=∠BCE,再根据矩形的性质及平行线的性质得出∠DEC=∠BCE,就可得到∠DEC=∠BEC,即可征得结论。
(2)根据角平分线的性质证明DE=EF,利用直角三角形全等的判定方法证明Rt△ECD≌Rt△ECF,得出CF=CD,再利用勾股定理求出AE的长,就可求出DE的长,再求出△ECD的面积,然后根据S四边形EFCD=2S△EDC , 即可求出结果。


科目:初中数学 来源: 题型:
【题目】综合题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
(![]() )如图①,已知线段
)如图①,已知线段![]() ,画出平面内满足
,画出平面内满足![]() 的所有点
的所有点![]() 组成的图形.
组成的图形.
问题探究:
(![]() )如图②,菱形
)如图②,菱形![]() 的对角线
的对角线![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 和
和![]() 上的动点,且
上的动点,且![]() ,点
,点![]() 为
为![]() 的中点,已知
的中点,已知![]() ,
, ![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 面积的最大值.
面积的最大值.
问题解决:
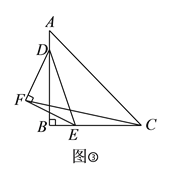
(![]() )如图③,等腰直角三角形
)如图③,等腰直角三角形![]() 的斜边
的斜边![]() ,点
,点![]() 、
、![]() 分别是直角边
分别是直角边![]() 和
和![]() 上的动点,以
上的动点,以![]() 为斜边在
为斜边在![]() 的左下侧(包括左侧和下侧)作等腰直角三角形
的左下侧(包括左侧和下侧)作等腰直角三角形![]() ,连接
,连接![]() ,则线段
,则线段![]() 的长度是否存在最小值,若存在,请求出这个最小值;若不存在,请说明理由.
的长度是否存在最小值,若存在,请求出这个最小值;若不存在,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=ax![]() +bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x
+bx+c的图象先向右平移3个单位,再向下平移2个单位,所得的图象的解析式是y=x![]() -3x+5,则a+b+c=__________。
-3x+5,则a+b+c=__________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.5 ![]()
B.25
C.10 ![]() +5
+5
D.35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com