
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,把一块含
,把一块含![]() 角的三角板
角的三角板![]() 的直角顶点
的直角顶点![]() 放在
放在![]() 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为![]() ,长直角边为
,长直角边为![]() ),点
),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
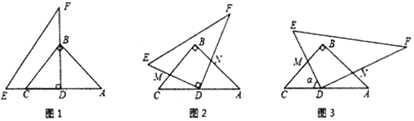
(1)求重叠部分![]() 的面积;
的面积;
(2)如图2,将直角三角板![]() 绕
绕![]() 点按顺时针方向旋转30度,
点按顺时针方向旋转30度,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
①请说明:![]() ;
;
②在此条件下,![]() 与直角三角板
与直角三角板![]() 重叠部分的面积会发生变化吗?请说明理由,并求出重叠部分的面积.
重叠部分的面积会发生变化吗?请说明理由,并求出重叠部分的面积.
(3)如图3,将直角三角板![]() 绕
绕![]() 点按顺时针方向旋转
点按顺时针方向旋转![]() 度(
度(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
【答案】(1)S△BCD=![]() ;(2)①证明见解析;②重叠部分的面积不变为
;(2)①证明见解析;②重叠部分的面积不变为![]() ;(3)DM=DN的结论仍成立,重叠部分面积不会变.
;(3)DM=DN的结论仍成立,重叠部分面积不会变.
【解析】
(1)重叠部分△BCD是一个等腰直角三角形,求出其直角边,即可求解;
(2)①连接BD,先证得BD=CD,∠C=∠NBD=45°,进而求出△CDM≌△BDN,即可得到DM=DN;②利用①中的结论△CDM≌△BDN即可得出答案;
(3)证明过程类似(2),根据(2)中的结论,可以直接写出.
解:(1)∵AB=BC,AC=2,D是AC的中点,∠ABC=90°,
∴∠BCD=∠A=∠CBD=45°,BD⊥AC.
∴CD=BD=![]() AC=1.
AC=1.
∴S△BCD=![]() CD·BD=
CD·BD=![]() ×1×1=
×1×1=![]() .
.
(2)①连接BD,
∵AB=BC,D是AC的中点,∠ABC=90°,
∴∠C=∠A=∠CBD=∠ABD=45°,
∴BD=CD,∠C=∠NBD=45°,
又∵直角三角板DEF绕D点按顺时针方向旋转30度,
∴∠CDM=∠BDN=30°,
∴△CDM≌△BDN(ASA).
∴DM=DN.
②由①知△CDM≌△BDN,
∴S四边形BNDM=S△BCD=![]() ,
,
即此条件下重叠部分的面积不变为![]() .
.
(3)DM=DN的结论仍成立,重叠部分面积不会变.(证明过程类似(2))



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读下列材料并完成任务:
中国古代三国时期吴国的数学家赵爽最早对勾股定理作出理论证明.他创制了一幅“勾股圆方图”(如图l),用数形结合的方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形![]() 是由
是由![]() 个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为
个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为![]() ;中间的小正方形边长为
;中间的小正方形边长为![]() ,面积为
,面积为![]() .于是便得到式子:
.于是便得到式子:![]() .赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中
.赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中![]() 、
、![]() 、
、![]() 和
和![]() 是四个全等的直角三角形,四边形
是四个全等的直角三角形,四边形![]() 和
和![]() 都是正方形,根据这个图形的面积关系,可以证明勾股定理.设
都是正方形,根据这个图形的面积关系,可以证明勾股定理.设![]() ,
,![]() ,
,![]() ,取
,取![]() ,
,![]() .
.
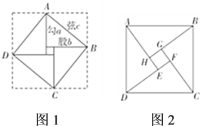
任务:
(1)填空:正方形![]() 的面积为______,四个直角三角形的面积和为______;
的面积为______,四个直角三角形的面积和为______;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)与x轴交于点(x1,0)与(x2,0),其中x1<x2,方程ax2+bx+c-a=0的两根为m,n(m<n),则下列判断正确的是( )
A. m<n<x1<x2 B. m<x1<x2<n C. x1+x2>m+n D. b2-4ac≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要制作一批宣传材料.甲公司提出:每份材料收费1元,另收取制版费600元;乙公司提出:每份材料收费1.2元,不收取制版费.
(1)设制作![]() 份宣传材料,甲公司收费
份宣传材料,甲公司收费![]() 元,乙公司收费
元,乙公司收费![]() 元,请分别写出
元,请分别写出![]() ,
,![]() 与
与![]() 的关系式;
的关系式;
(2)该单位要制作宣传材料1000~4500(含1000和4500)份,选择哪家公司比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有三个点A、B、C,完成系列问题:
(1)将点B向右移动六个单位长度到点D,在数轴上表示出点D.
(2)在数轴上找到点E,使点E到A、C两点的距离相等.并在数轴上标出点E表示的数.
(3)在数轴上有一点F,满足点F到点A与点F到点C的距离和是9,则点F表示的数是 .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学从学生入学开始就积极开展环保教育,半学期后随机对部分学生的环保习惯养成情况进行了问卷调查,问卷中的环保习惯有:①随手关灯;②充电后及时拔充电器插头;③生活用水合理重复利用;④不用或少用一次性餐具;⑤少用塑料袋多用环保袋;⑥绿色出行,同学勾选出自己已经养成的环保习惯,学校将结果绘成了如图所示的不完整的条形统计图和扇形统计图.
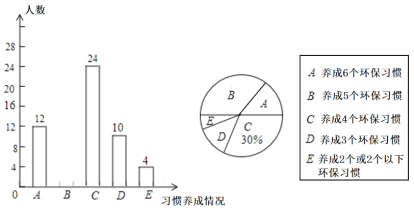
(1)求在这次调查中,一共抽查了多少名学生?
(2)通过计算补全条形统计图.
(3)已知全校共有学生1200人,请估计全校所有学生中已经养成3个或3个以上环保习惯的同学共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连接BD,过点E作EH⊥BD,垂足为H,连接EF,交BD于点G,交BC于点M,连接CF. 给出下列结论:①△CDE∽△CBF;②∠DBC=∠EFC;③ ![]() ;④GH的值为定值
;④GH的值为定值![]() ;上述结论中正确的个数为( )
;上述结论中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com