
分析 先利用因式分解法分别解两个一元二次方程得到p和q的值,然后计算它们的差即可.
解答 解:∵(2016x)2-(2015×2017)x-1=0,
∴(20162x+1)(x-1)=0,
∴x1=-$\frac{1}{2016}$,x2=1,则p=1,
2015x2-2016x+1=0,
(2015x-1)(x-1)=0,
∴x1=$\frac{1}{2015}$,x2=1,则q=$\frac{1}{2015}$,
∴p-q=1-$\frac{1}{2015}$=$\frac{2014}{2015}$.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.也考查了因式分解法解一元二次方程.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | a2+a3=a5 | C. | $\frac{1}{y}$-$\frac{1}{x}$=x-y | D. | (-a3b)2=a6b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,长方体的长为4厘米,宽为3厘米,高为5厘米.
如图,长方体的长为4厘米,宽为3厘米,高为5厘米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
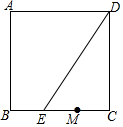 如图,在正方形ABCD中,AB=6,点E、M是边BC的三等分点,连结DE,将△DEC以点M为旋转中心顺时针旋转,当点D的对应点D‘恰好落在正方形的一条边上时,AD‘的长为2或$6-2\sqrt{6}$.
如图,在正方形ABCD中,AB=6,点E、M是边BC的三等分点,连结DE,将△DEC以点M为旋转中心顺时针旋转,当点D的对应点D‘恰好落在正方形的一条边上时,AD‘的长为2或$6-2\sqrt{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com