
【题目】计算:
(1)先化简,再求值:(3x2﹣4)+(2x2+5x﹣6)﹣2(x2﹣5),其中x=﹣2
(2)解方程: ![]() ﹣
﹣ ![]() =2.
=2.
【答案】
(1)解:原式=3x2﹣4+2x2+5x﹣6﹣2x2+10=3x2+5x,
当x=﹣2时,原式=3×(﹣2)2+5×(﹣2)=12﹣10=2
(2)解:去分母,得2×(2x+1)﹣(x+1)=12,
去括号,得4x+2﹣x﹣1=12,
移项,合并同类项,得3x=11,
系数化为1得x= ![]()
【解析】(1)根据同类项的定义和合并同类项的法则可将代数式化简,再代值计算;(2)依次按照解方程的步骤去分母,去括号,移项,合并同类项,系数化为1计算即可。
【考点精析】利用解一元一次方程的步骤和代数式求值对题目进行判断即可得到答案,需要熟知先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了;求代数式的值,一般是先将代数式化简,然后再将字母的取值代入;求代数式的值,有时求不出其字母的值,需要利用技巧,“整体”代入.


科目:初中数学 来源: 题型:
【题目】某通讯公司推出①、②两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.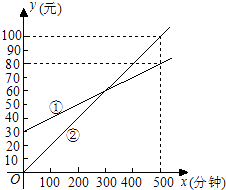
(1)有月租费的收费方式是(填①或②),月租费是元;
(2)分别求出①、②两种收费方式中y与自变量x之间的函数关系式;
(3)请你根据用户通讯时间的多少,给出经济实惠的选择建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F. 
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,与
,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:

①![]() ;② 方程
;② 方程![]() 的两个根是
的两个根是![]() ;③
;③ ![]() ;④当
;④当![]() 时,
时, ![]() 的取值范围是
的取值范围是![]() ;⑤ 当
;⑤ 当![]() 时,
时, ![]() 随
随![]() 增大而增大;其中结论正确有____.
增大而增大;其中结论正确有____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com