
【题目】如图所示,直线a 、b被直线c所截,现给出下列四种条件:
①∠2=∠6 ②∠2=∠8 ③∠1+∠4=180° ④∠3=∠8,其中能判断是a∥b的条件的序号是( )
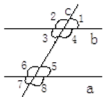
A. ①② B. ①③ C. ①④ D. ③④
科目:初中数学 来源: 题型:
【题目】已知如图为一几何体的三视图:主视图和左视图都是长方形,俯视图是等边三角形
(1)写出这个几何体的名称;
(2)若主视图的高为10cm,俯视图中三角形的边长为4cm,求这个几何体的侧面积.
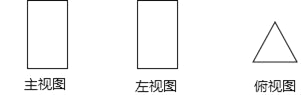
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形ECGF都是正方形,点C、D、E在一条直线上,点B、C、G在一条直线上.
(1)写出表示阴影部分面积的表达式(结果要求化简);
(2)当![]() 求阴影面积的面积
求阴影面积的面积

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=135°,将一个含45°角的直角三角尺的一个顶点放在点O处,斜边OM与直线AB重合,另外两条直角边都在直线AB的下方.

(1)将图1中的三角尺绕着点O逆时针旋转90°,如图2所示,此时∠BOM=_____;在图2中,OM是否平分∠CON?请说明理由;
(2)紧接着将图2中的三角板绕点O逆时针继续旋转到图3的位置所示,使得ON在∠AOC的内部,请探究:∠AOM与∠CON之间的数量关系,并说明理由;
(3)将图1中的三角板绕点O按每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,A、B两点之间的距离是90米,甲、乙两机器人分别从A、B两点同时同向出发到终点C,乙机器人始终以50米分的速度行走,乙行走9分钟到达C点.设两机器人出发时间为t(分钟),当t=3分钟时,甲追上乙.
请解答下面问题:
(1)B、C两点之间的距离是 米.
(2)求甲机器人前3分钟的速度为多少米/分?
(3)若前4分钟甲机器人的速度保持不变,在4≤t≤6分钟时,甲的速度变为与乙相同,求两机器人前6分钟内出发多长时间相距28米?
(4)若6分钟后甲机器人的速度又恢复为原来出发时的速度,直接写出当t>6时,甲、乙两机器人之间的距离S.(用含t的代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D、E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.
(1)判断∠ABE与∠ACD的数量关系,并说明理由;
(2)求证:过点A、F的直线垂直平分线段BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(数学阅读)
如图1,在△ABC中,AB=AC,点P为边BC上的任意一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F,求证:PD+PE=CF.
小尧的证明思路是:如图2,连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
(推广延伸)
如图3,当点P在BC延长线上时,其余条件不变,请运用上述解答中所积累的经验和方法,猜想PD,PE与CF的数量关系,并证明.
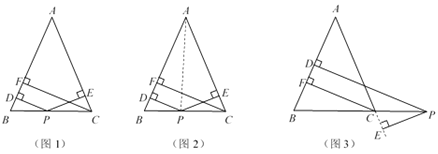
(解决问题)
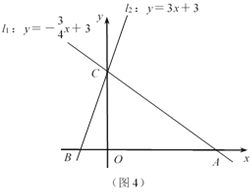
如图4,在平面直角坐标系中有两条直线l1:y=-![]() x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.
x+3,l2:y=3x+3,l1,l2与x轴的交点分别为A,B.
(1)两条直线的交点C的坐标为 ;
(2)说明△ABC是等腰三角形;
(3)若l2上的一点M到l1的距离是1,运用上面的结论,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于点C,连接BC,如果∠A=30°,AB=2 ![]() ,那么AC的长等于( )
,那么AC的长等于( )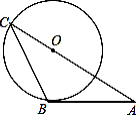
A.4
B.6
C.4 ![]()
D.6 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com