
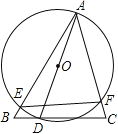
【题目】如图,△ABC中,∠B=60,∠ACB=75,点D是BC边上一动点,以AD为直径作⊙O,分别交AB、AC于E、F,若弦EF的最小值为1,则AB的长为
A. | B. | C.1.5 | D. |
【答案】B
【解析】
首先连接OE,OF,过O点作OH⊥EF,垂足为H,可求得半径OE的长,又由当AD为△ABC的边BC上的高时,AD最大时为直径,OE最大,OH最大,EF最小,可求得AD的长,由三角函数的性质,即可求得AB的长.
 解:如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
解:如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
∴EH=FH=![]() EF=
EF=![]() ×1=
×1=![]() ,
,
∵在△ADB中,∠B=60°,∠ACB=75°,
∴∠BAC=45°,
∴∠EOF=2∠BAC=90°,
∵OE=OF,
∴∠EOH=![]() ∠EOF=45°,
∠EOF=45°,
∴OE=![]() =
=![]() ,
,
∵当AD为△ABC的边BC上的高时,AD最大时为直径,OE最大,OH最大,EF最小,
∴AD=2OE=![]() ,
,
∴AB=![]() =
=![]()
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:如图.在△ABC中.AB=AC=5cm,BC=6cm.点P由B出发,沿BC方向匀速运动.速度为1cm/s.同时,点Q从点A出发,沿AC方向匀速运动.速度为1cm/s,过点P作PM![]() BC交AB于点M,过点Q作QN
BC交AB于点M,过点Q作QN![]() BC,垂足为点N,连接MQ,若设运动时间为t(s)(0<t<3),解答下列问题:
BC,垂足为点N,连接MQ,若设运动时间为t(s)(0<t<3),解答下列问题:
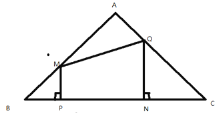
(1)当t为何值时,点M是边AB中点?
(2)设四边形PNQM的面积为y(cm2),求出y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形PNQM:S△ABC=4:9?若存在,求出此时t的值;若不存在,说明理由;
(4)是否存在某一时刻t,使四边形PNQM为正方形?若存在,求出此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
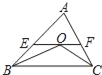
【题目】如图,在△ABC中,点O是∠ABC和∠ACB两个内角平分线的交点,过点O作EF∥BC分别交AB,AC于点E,F,已知△ABC的周长为8,BC=x,△AEF的周长为y,则表示y与x的函数图象大致是( )
A.  B.
B. 
C. 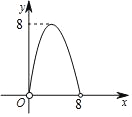 D.
D. 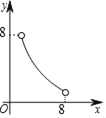
查看答案和解析>>
科目:初中数学 来源: 题型:
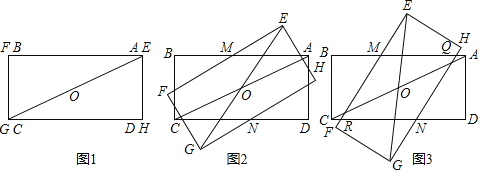
【题目】综合与实践:矩形的旋转
问题情境:
在综合与实践课上,老师让同学们以“矩形的旋转”为主题开展数学活动.具体要求:如图1,将长与宽都相等的两个矩形纸片ABCD和EFGH叠放在一起,这时对角线AC和EG互相重合.固定矩形ABCD,将矩形EFGH绕AC的中点O逆时针方向旋转,直到点E与点B重合时停止,在此过程中开展探究活动.
操作发现:
(1)雄鹰小组初步发现:在旋转过程中,当边AB与EF交于点M,边CD与GH交于点N,如图2、图3所示,则线段AM与CN始终存在的数量关系是 .
(2)雄鹰小组继续探究发现:在旋转开始后,当两个矩形纸片重叠部分为四边形QMRN时,如图3所示,四边形QMRN为菱形,请你证明这个结论.
(3)雄鹰小组还发现在问题(2)中的四边形QMRN中∠MQN与旋转角∠AOE存在着特定的数量关系,请你写出这一关系,并说明理由.
实践探究:
(4)在图3中,随着矩形纸片EFGH的旋转,四边形QMRN的面积会发生变化.若矩形纸片的长为![]() ,宽为
,宽为![]() ,请你帮助雄鹰小组探究当旋转角∠AOE为多少度时,四边形QMRN的面积最大?最大面积是多少?(直接写出答案)
,请你帮助雄鹰小组探究当旋转角∠AOE为多少度时,四边形QMRN的面积最大?最大面积是多少?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,水平地面上有一幢高为AD的楼,楼前有坡角为30°、长为6米的斜坡.已知从A点观测B、C的俯角分别为60°和30°
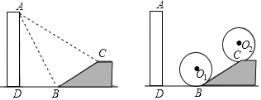
(1)求楼高;
(2)现在要将一个半径为2米的⊙O从坡底与斜坡相切时的⊙O1位置牵引滚动到斜坡上至圆刚好与斜坡上水平面相切时的⊙O2位置,求滚动过程中圆心O移动的总长度.(参考数据:tan15°=2﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线.交BC于点E.
(1)求证:BE=EC
(2)填空:①若∠B=30°,AC=2![]() ,则DB= ;
,则DB= ;
②当∠B= 度时,以O,D,E,C为顶点的四边形是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
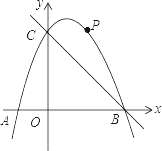
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,OA=8,OC=4,OA、OC分别在x轴与y轴上,D为OA上一点,且CD=AD.
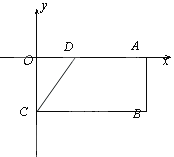
(1)求点D的坐标;
(2)若经过B、C、D三点的抛物线与x轴的另一个交点为E,请直接写出点E的坐标;
(3)在(2)中的抛物线上位于x轴上方的部分,是否存在一点P,使△PBC的面积等于梯形DCBE的面积?若存在,求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com