Question

15．（1）如图（1），在Rt△ABC中，∠ACB=90°，∠B=60°，在图中作出∠ACB的三等分线CD，CE．（要求：尺规作图，保留作图痕迹，不写作法）
（2）由（1）知，我们可以用尺规作图作出直角的三等分线，但是仅仅使用尺规却不能把任意一个角分成三等分，为此，人们发明了许多等分角的机械器具，如图（2）是用三张硬纸片自制的一个最简单的三分角器，与半圆O相接的AB带的长度与半圆的半径相等；BD带的长度任意，它的一边与直线AC形成一个直角，且与半圆相切于点B，假设需要将∠KSM三等分，如图（3），首先将角的顶点S置于BD上，角的一边SK经过点A，另一边SM与半圆相切，连接SO，则SB，SO为∠KSM的三等分线，请你证明．

Answer 1

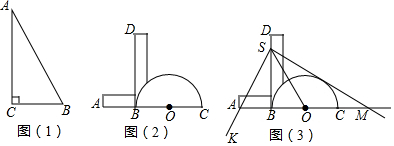
分析 （1）如图射线CD、CE为所求是三等分线；
（2）如图，设SM与半圆O相切于点N，连接ON．则∠ONS=90°，只要证明△SBA≌△SBO，△SOB≌△SON，即可解决问题；

解答 解：（1）如图射线CD、CE为所求是三等分线．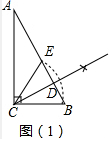


（2）如图，设SM与半圆O相切于点N，连接ON．则∠ONS=90°，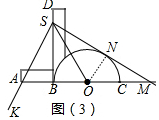

∵DB⊥AC，DB与半圆相切于点BM，
∴∠ABS=∠OBS=90°，
∵BA=BO．SB=SB，
∴△SBA≌△SBO，
∴∠ASB=∠BSO，
∵SO=SO．OB=ON，∠SBO=∠SNO，
∴△SBO≌△SNO，
∴∠BSO=∠OSN，
∴∠ASB=∠BSO=∠OSC，
∴SB，SO为∠KSM的三等分线．

点评 本题考查作图-复杂作图、全等三角形的判定和性质、切线的性质等知识，解题的关键是少林足球五种基本作图，学会添加常用辅助线，构造全等三角形解决问题．