
 如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.
如图,为美化环境,某小区计划在一块长为60m,宽为40m的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建同样宽的通道,当通道的面积与花圃的面积之比等于3:5时,求此时通道的宽.  数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:填空题
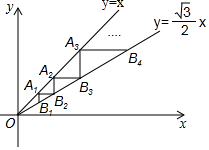 如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B3,…,按照此规律进行下去,则点An的横坐标为$(\frac{2\sqrt{3}}{3})^{n-1}$.
如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线y=$\frac{\sqrt{3}}{2}$x于点B3,…,按照此规律进行下去,则点An的横坐标为$(\frac{2\sqrt{3}}{3})^{n-1}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
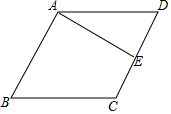 如图,作菱形ABCD的高AE,E为CD的中点.AE=$\sqrt{3}$cm,则菱形ABCD的周长是( )
如图,作菱形ABCD的高AE,E为CD的中点.AE=$\sqrt{3}$cm,则菱形ABCD的周长是( )| A. | 4$\sqrt{3}$cm | B. | 4$\sqrt{2}$cm | C. | 4cm | D. | 8cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com