

分析 (1)先根据PM∥NQ,得出内错角相等,再根据AAS或ASA判定△PMO≌△QNO即可;
(2)如图2,分别延长DC、AE,交于G点,根据已知条件可以得到△ABE≌△GCE,由此得到AB=CG,又AB∥DC,∠BAE=∠EAF,利用平行线的性质和等腰三角形的判定定理可以证明AF=GF,利用这些即可证明题目的结论.
解答 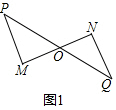 解:(1)如图1,∵点O为线段MN的中点,
解:(1)如图1,∵点O为线段MN的中点,
∴MO=NO,
∵PM∥NQ,
∴∠P=∠Q,∠M=∠N,
在△PMO和△QNO中,
$\left\{\begin{array}{l}{∠P=∠Q}\\{∠M=∠N}\\{MO=NO}\end{array}\right.$,
∴△PMO≌△QNO(AAS);
(2)AB=AF+CF.
如图2,分别延长DC、AE,交于G点,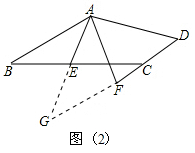
根据图①得,△ABE≌△GCE,
∴AB=CG,
又∵AB∥DC,
∴∠BAE=∠G
而∠BAE=∠EAF,
∴∠G=∠EAF,
∴AF=GF,
∴AB=CG=GF+CF=AF+CF.
点评 此题主要考查了全等三角形的性质与判定及相似三角形的性质与判定,此题是探究题目,首先正确理解给出的基本图形的隐含结论,然后结合要探究的图形作辅助线把探究的问题转换为已知的问题解决即可.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:解答题
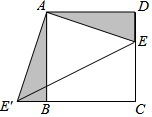 如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE'.
如图,已知正方形ABCD的边长为3,E为CD边上一点,DE=1.以点A为中心,把△ADE顺时针旋转90°,得△ABE',连接EE'.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
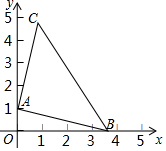 如图,已知点A(0,1),点B是x轴正半轴上一动点,以AB为边作等腰直角三角形ABC,使点C在第一象限,∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,则表示y与x的函数关系的图象大致是( )
如图,已知点A(0,1),点B是x轴正半轴上一动点,以AB为边作等腰直角三角形ABC,使点C在第一象限,∠BAC=90°.设点B的横坐标为x,点C的纵坐标为y,则表示y与x的函数关系的图象大致是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{3}$与$\frac{1}{3}$ | B. | -3与3 | C. | $\frac{1}{3}$与3 | D. | -3与$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
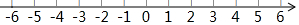 邮递员骑摩托车从邮局出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行9km到C村,最后回到邮局.
邮递员骑摩托车从邮局出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行9km到C村,最后回到邮局.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com