
分析 (1)设y=kx+b,把已知坐标代入求出函数关系式.
(2)由已知得w=xy-0.5y=-x2+3.5x-1.5.求出顶点坐标即可.
解答 解:(1)设销售量y(吨)与每吨的销售价x(万元)之间的函数关系式y=kx+b,
∵已知x=0.6时,y=2.4;x=1时,y=2,
∴$\left\{\begin{array}{l}{0.6k+b=2.4}\\{k+b=2}\end{array}\right.$
∴$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$.
∴函数关系式为y=-x+3;
(2)∵由已知w=y•x-y×0.5=(-x+3)x-(-x+3)×0.5=-x2+3.5x-1.5,
∴w与x之间的函数关系式是w=-x2+3.5x-1.5,
∵0.5×2≤x≤0.5×4,即1≤x≤2,
由w=-x2+3.5x-1.5可知当x=-$\frac{3.5}{-1×2}$=$\frac{7}{4}$时,函数有最大值,
∴销售价定为1.75万元时能获得最大销售利润.
点评 本题考查的是二次函数的实际应用.待定系数法求得y与x的函数关系式是关键.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若a=b,则a+c=b+c | B. | 若a+c=b+c,则a=b | C. | 若a=b,则ac=bc | D. | 若ac=bc,则a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把一张矩形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=8cm,BC=16cm.
把一张矩形纸片按如图方式折叠,使顶点B和点D重合,折痕为EF.若AB=8cm,BC=16cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
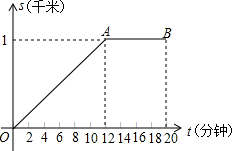 小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.
小明与小刚住在同一居民楼,小明早晨从家里出发匀速步行上学,小刚在小明出发10分钟后,匀速骑车按小明上学的路线去上学,结果在小明出发20分钟后他们同时到达学校.已知小明距离家的距离S(km)与小明出发时间t(分)的图象为图中的折线OA-AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com