
 如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是________.
如图所示边长是6的等边三角形纸片,撕成了不规则的甲、乙两部分,两张纸片间隔的水平距离是2,则中间留有空隙部分的面积是________.
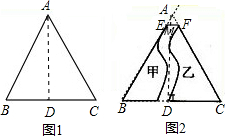 解:如图1,原等边三角形纸片为△A′B′C′,作A′D′⊥B′C′,
解:如图1,原等边三角形纸片为△A′B′C′,作A′D′⊥B′C′,
 ,
, ,AD=4
,AD=4 ,
, ,S△AEF=
,S△AEF= ,
, -9
-9 =6
=6 .
. .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图所示,△OAB是边长为2+
如图所示,△OAB是边长为2+| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:044
(2004·河北鹿泉)如图所示,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网格的底部重合时,继续以同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动,设运动时间为x秒,△QAC的面积为y.
(1)如图所示,当Rt△ABC向下平移到 的位置时,请你在网格图中画出
的位置时,请你在网格图中画出 关于直线QN成轴对称的图形;
关于直线QN成轴对称的图形;

(2)如图所示,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?

(3)在Rt△ABC向右平移的过程中,请你说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com