
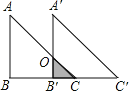
【题目】如图所示,已知Rt△ABC中,∠B=90°,BC=4,AB=4,现将△ABC沿BC方向平移到△A′B′C′的位置.若平移的距离为3,则△ABC与△A′B′C′重叠部分的阴影面积为__.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() ;D为
;D为![]() 边上的动点.
边上的动点.
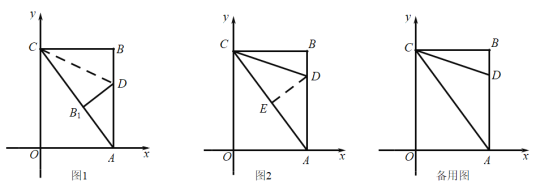
(Ⅰ)如图1,将![]() 对折,使得点B的对应点
对折,使得点B的对应点![]() 落在对角线
落在对角线![]() 上,折痕为
上,折痕为![]() ,求此刻点D的坐标;
,求此刻点D的坐标;
(Ⅱ)如图2,将![]() 对折,使得点A的与点C重合,折痕交
对折,使得点A的与点C重合,折痕交![]() 于点D,交
于点D,交![]() 于点E,求直线
于点E,求直线![]() 的解析式;
的解析式;
(Ⅲ)在坐标平面内,是否存在点P(除点B外),使得![]() 与
与![]() 全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
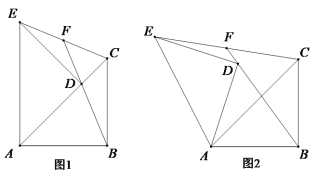
【题目】已知在Rt△ABC中,∠ABC=90°,AB=BC,将△ABC绕点A逆时针方向旋转,得到△ADE,旋转角为α(0°<α<90°),直线BD与CE交于点F.
(1)如图1,当α=45°时,求证:CF=EF;
(2)如图2,在旋转过程中,当α为任意锐角时,
① ∠CFB的度数是否变化?若不变,请求出它的度数;
② 结论“CF=EF”,是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点A(﹣5,0)作垂直于x轴的直线AB,直线y=x+b与双曲线y=﹣![]() 相交于点P(x1,y1)、Q(x2,y2),与直线AB相交于点R(x3,y3).若y1>y2>y3时,则b的取值范围是( )
相交于点P(x1,y1)、Q(x2,y2),与直线AB相交于点R(x3,y3).若y1>y2>y3时,则b的取值范围是( )
A.b>4B.b>4或b<﹣4
C.﹣![]() <b<﹣4或b>4D.4<b<
<b<﹣4或b>4D.4<b<![]() 或b<﹣4
或b<﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则称这个点为“美好点”,如图,过点P分别作x轴,y轴的垂线,与坐标轴围成的矩形OAPB的周长与面积相等,则P为“美好点”.

(1)在点M(2,2),N(4,4),Q(﹣6,3)中,是“美好点”的有 ;
(2)若“美好点”P(a,﹣3)在直线y=x+b(b为常数)上,求a和b的值;
(3)若“美好点”P恰好在抛物线y=![]() x2第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
x2第一象限的图象上,在x轴上是否存在一点Q使得△POQ为直角三角形?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
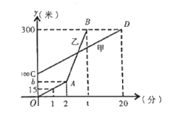
【题目】甲乙两人同时登同一座山,甲乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)乙在提速前登山的速度是______米/分钟,乙在![]() 地提速时距地面的高度
地提速时距地面的高度![]() 为 __________米.
为 __________米.
(2)若乙提速后,乙比甲提前了9分钟到达山顶,请求出乙提速后![]() 和
和![]() 之间的函数关系式.
之间的函数关系式.
(3)登山多长时间时,乙追上了甲,此时甲距![]() 地的高度为多少米?
地的高度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有 150 名女生,为了解该年级女生实心球成绩(单位:米)和一分钟仰卧起坐成绩(单位:个)的情况,从中随机抽取 30 名女生进行测试,获得了她们的相关成绩,并对数据进行了整理,下面给出了部分信息.
a.实心球成绩的频数分布如表所示:

b.实心球成绩在 7.0≤x<7.4 这一组的是:7.0,7.0,7.0,7.1,7.1,7.1,7.2,7.2,7.3,7.3
c.一分钟仰卧起坐成绩如图所示:
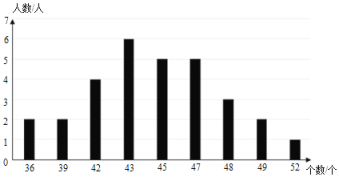
根据以上信息,回答下列问题:
(1)①表中 m 的值为 ;②一分钟仰卧起坐成绩的中位数为 ;
(2)若实心球成绩达到 7.2 米及以上时,成绩记为优秀.
①请估计全年级女生实心球成绩达到优秀的人数;
②该年级某班体育委员将本班在这次抽样测试中被抽取的 8 名女生的两项成绩的数据抄录如表所示:

其中有 3 名女生的一分钟仰卧起坐成绩未抄录完整,但老师说这 8 名女生中恰好有4 人两项测试成绩都达到了优秀,于是体育委员推测女生 E 的一分钟仰卧起坐成绩达到了优秀,你是否同意体育委员的说法? (填“是”或“否”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
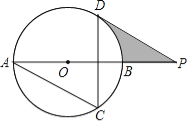
(1)求证:DP是⊙O的切线;
(2)若⊙O的半径为3cm,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知A、B、C是⊙O上的三点,AB=AC,∠BAC=120°.
(1)求证:⊙O的半径R=AB;
(2)如图2,若点D是∠BAC所对弧上的一动点,连接DA,DB,DC.
①探究DA,DB,DC三者之间的数量关系,并说明理由;
②若AB=3,点C'与C关于AD对称,连接C'D,点E是C'D的中点,当点D从点B运动到点C时,求点E的运动路径长.
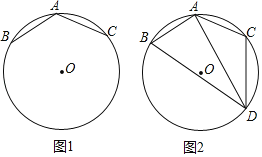
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com