
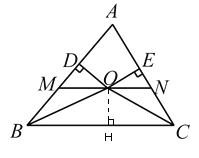
【题目】已知:如图,在△ABC中,∠ABC、∠ACB的平分线相交于点O,MN过点O,且MN∥BC,分别交AB、AC于点M、N.OD⊥AB,OE⊥AC.
(1)求证:OD=OE.
(2)若O为MN的中点,判断△ABC的形状,并说明理由.

【答案】(1)证明见解析;(2)等腰三角形.
【解析】
(1)作OH⊥BC,根据角平分线的性质得到OD=OH,OE=OH,故OD=OE.
(2)根据O点为MN中点得到OM=ON,根据HL可证明Rt△MOD≌Rt△NOE,得到∠AMN=∠ANM,再根据平行得到∠ABC=∠ACB,即可得到△ABC为等腰三角形.
(1)作OH⊥BC,
∵∠ABC、∠ACB的平分线相交于点O,OD⊥AB,OE⊥AC.
∴OD=OH,OE=OH,
故OD=OE.
(2)∵O点为MN中点
∴OM=ON,
∵OD⊥AB,OE⊥AC.
∴△MOD与△NOE为Rt△,
又OD=OE,
∴Rt△MOD≌Rt△NOE(HL)
∴∠AMN=∠ANM,
∵MN∥BC
∴∠ABC=∠ACB,
故△ABC为等腰三角形.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:
【题目】我们知道“对称补缺”的思想是解决与轴对称图形有关的问题的一种重要的添加辅助线的策略,参考这种思想解决下列问题.
在△ABC中,D为△ABC外一点.

(1)如图1,若AC平分∠BAD,CE⊥AB于点E,∠ B+∠ADC=180,求证:BC=CD;
(2)如图2,若∠ACB=90°, AC=BC,F是AC上一点,AD⊥BF交BF延长线于点D,且BF是∠CBA的角平分线.求证:2AD=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.

(1)作出△ABC关于y轴对称的△A1B1C1,其中A,B,C分别和A1,B1,C1对应;
(2)平移△ABC,使得A点在x轴上,B点在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中A,B,C分别和A2,B2,C2对应;
(3)填空:在(2)中,设原△ABC的外心为M,△A2B2C2的外心为M,则M与M2之间的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b分别交y轴、x轴于C、D两点,与反比例函数y=![]() (x>0)的图象交于A(m,8),B(4,n)两点.
(x>0)的图象交于A(m,8),B(4,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() <0的x的取值范围;
<0的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:已知∠MAB=60°,以AB的长为菱形ABCD的边长,点D在AM上,
(1)作出这个菱形.(保留作图痕迹,不写作法,不用证明)
(2)若AB=2,则对角线AC的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距20km.甲、乙两人都由A地去B地,甲骑自行车,平均速度为10km/h;乙乘汽车,平均速度为40km/h,且比甲晚1.5h出发.设甲的骑行时间为x(h)(0≤x≤2)
(1)根据题意,填写下表:
时间x(h) 与A地的距离 | 0.5 | 1.8 | _____ |
甲与A地的距离(km) | 5 |
| 20 |
乙与A地的距离(km) | 0 | 12 |
|
(2)设甲,乙两人与A地的距离为y1(km)和y2(km),写出y1,y2关于x的函数解析式;
(3)设甲,乙两人之间的距离为y,当y=12时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴. 如果
轴. 如果![]() 三个顶点的坐标分别是
三个顶点的坐标分别是![]() ,
,![]() ,
,![]() ,
,![]() 关于直线
关于直线![]() 的对称图形是
的对称图形是![]() .
.

(1)画出![]()
(2)直接写出![]() 、
、![]() 、
、![]() 的坐标.
的坐标.
(3)求出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的边AB上,且AD=CD,
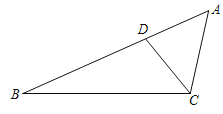
(1)用直尺和圆规作∠BDC的平分线DE,交BC于点E(不写作法,保留作图痕迹);
(2)在(1)的条件下,判断DE与AC的位置关系,并写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com