
【题目】某长途汽车客运公司规定旅客可以免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)与行李质量x(kg)之间的函数表达式为 ![]() ,这个函数的图像如图所示,求:
,这个函数的图像如图所示,求:
(1)k和b的值;
(2)旅客最多可免费携带行李的质量;
(3)行李费为4~15元时,旅客携带行李的质量为多少?
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,将正方形向上平移3个单位后,得到的正方形各顶点与原正方形各顶点坐标相比( )
A.横坐标不变,纵坐标加3
B.纵坐标不变,横坐标加3
C.横坐标不变,纵坐标乘以3
D.纵坐标不变,横坐标乘以3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠C=90°,AC=BC=![]() ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
(1)请你在图中把图补画完整;
(2)求C′B的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知Rt△ABC≌Rt△ADE,其中∠ACB=∠AED=90°.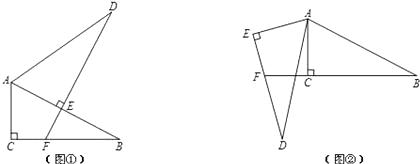
(1)将这两个三角形按图①方式摆放,使点E落在AB上,DE的延长线交BC于点F.求证:BF+EF=DE;
(2)改变△ADE的位置,使DE交BC的延长线于点F(如图②),则(1)中的结论还成立吗?若成立,加以证明;若不成立,写出此时BF、EF与DE之间的等量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
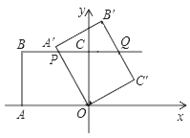
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(-8,0),直线BC经过点B(-8,6),C(0,6),将四边形OABC绕点O按顺时针方向旋转α度(0<α ≤180°)得到四边形OA′B′C′,此时直线OA′、直线B′C′分别与直线BC相交于P、Q.在四边形OABC旋转过程中,若BP=![]() BQ,则点P的坐标为__________.
BQ,则点P的坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com