
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
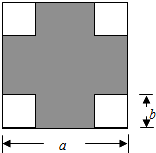 在一块边长为a的正方形纸板的四个角上各剪去一个边长为b(b<$\frac{a}{2}$)的小正方形.做一个无盖长方形,长方形所用的纸板的面积(图中阴影部分)是多少?当a=22.4,b=7.6时,这个面积的值又是多少?请利用分解因式的方法计算.
在一块边长为a的正方形纸板的四个角上各剪去一个边长为b(b<$\frac{a}{2}$)的小正方形.做一个无盖长方形,长方形所用的纸板的面积(图中阴影部分)是多少?当a=22.4,b=7.6时,这个面积的值又是多少?请利用分解因式的方法计算.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.
如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com