
【题目】如图,矩形ABCD中,AB=4,BC=2,O为对角线AC的中点,点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,图中阴影部分面积的大小变化情况是( )

A. 一直增大 B. 一直减小 C. 先减小后增大 D. 先增大后减小
【答案】C
【解析】连接OB,根据点O是为对角线AC的中点可得△ABO和△BOC的面积相等,又点P、Q分别从A和B两点同时出发,在边AB和BC上匀速运动,并且同时到达终点B、C,连接PO、QO并延长分别与CD、DA交于点M、N.在整个运动过程中,然后把开始时、结束时、与中点时的△OPQ的面积与△ABC的面积相比即可进行判断.
解:如图所示,
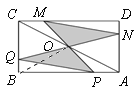
连接OB,∵O是AC的中点,
∴S△ABO=S△BOC=![]() S△ABC,
S△ABC,
开始时,S△OBP=S△AOB=![]() S△ABC,
S△ABC,
点P到达AC的中点时,点Q到达BC的中点时,S△OPQ=![]() S△ABC,
S△ABC,
结束时,S△OPQ=S△BOC=![]() S△ABC,
S△ABC,
所以,图中阴影部分面积的大小变化情况是:先减小后增大.
故选C.
“点睛“本题考查了动点问题的函数图象,根据题意找出关键的开始时,中点时,结束时三个时间点的三角形的面积与△ABC的面积的关系是解题的关键.


科目:初中数学 来源: 题型:
【题目】要在一块长52 m,宽48 m的矩形绿地上,修建同样宽的两条互相垂直的甬路,下面分别是小亮和小颖的设计方案.
(1)求小亮设计方案中甬路的宽度x;
(2)求小颖设计方案中四块绿地的总面积.(友情提示:小颖设计方案中的x与小亮设计方案中的x取值相同)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师出了一道题:化简
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3].
小明同学马上举手,下面是小明的解题过程:
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]÷8(a+b)3
=(a+b)2-![]() (a+b)+
(a+b)+ ![]() .
.
小亮也举起了手,说小明的解题过程不对,并指了出来.老师肯定了小亮的回答.你知道小明错在哪儿吗?请指出来,并写出正确解答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,已知等腰
,已知等腰![]() 在平面直角坐标系中,顶点
在平面直角坐标系中,顶点![]() 在
在![]() 轴上,直角顶点
轴上,直角顶点![]() 在
在![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的解析式为
的解析式为![]() .
.
(![]() )求直线
)求直线![]() 的函数解析式.
的函数解析式.
(![]() )如图
)如图![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,延长
,延长![]() 至点
至点![]() ,使
,使![]() ,连结
,连结![]() ,求证:
,求证: ![]() .
.
(![]() )如图
)如图![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,已知点
,已知点![]() 的坐标为
的坐标为![]() ,在直线
,在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的面积是
的面积是![]() 面积的
面积的![]() ,若存在,请求出点
,若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,问A型节能灯最多可以买多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,过点D作DF⊥BC,垂足为F,DF与AC交于点M,已知∠1=∠2.
(1)求证:CM=DM;
(2)若FB=FC,求证:AM-MD=2FM.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com