
分析 (1)根据花费的钱数=领取钱数-剩余钱数即可求出李老师花去的钱数,设8元的书买了x本,则12元的书买了(105-x)本,根据总价=8×8元书的购买数量+12×12元书的购买数量即可得出关于x的一元一次方程,解之即可得出x的值,根据x不是整数即可得出李老师搞错了;
(2)由笔记本的单价为小于8元的正整数即可得出关于x的一元一次不等式,解之即可得出x的取值范围,由x为整数即可得出x值,将其代入8x+12(105-x)中即可得出买书花的钱数,用花费的钱数减去买书花的钱数即可得出笔记本的单价.
解答 (1)解:设8元的买了x本,12元的是(105-x)本
∴一共花了:8x+12×(105-x)=1400-318,
8x-12x+1260=1082,
4x=178,
x=44.5(不符合题意).
∴不能整除,所以错了;
(2)设买的8元的书为x本,那么12的书为(105-x)本,水笔为a元,
∴1400-8x-12(105-x)-a=318.
4x-a=178
x=$\frac{178+a}{4}$
x=44+$\frac{2+a}{4}$
又x为正整数,且a为小于8正整数
∴(2+a)必须被4整数.
∴a=2或6.
∴水笔的价格为2元或6元
点评 本题考查了一元一次不等式的应用以及一元一次方程的应用,解题的关键是:(1)根据总价=单价×数量列出关于x的一元一次方程;(2)根据买书的钱数=花费的钱数-笔记本的钱数列出关于x的一元一次不等式.


科目:初中数学 来源: 题型:解答题
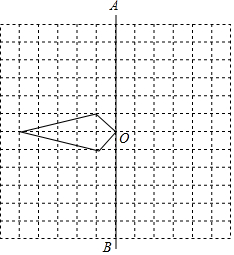 如图,在边长为1个单位长度的小正方形组成的12×10的长方形网格中有一四边形,请你解决下列问题:
如图,在边长为1个单位长度的小正方形组成的12×10的长方形网格中有一四边形,请你解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
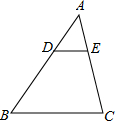 如图,在△ABC中,DE∥BC,若AD=2,DB=4,则$\frac{DE}{BC}$的值为( )
如图,在△ABC中,DE∥BC,若AD=2,DB=4,则$\frac{DE}{BC}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
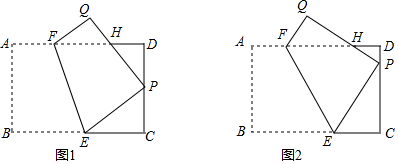
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
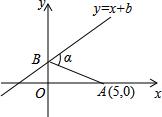 如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )| A. | 3 | B. | $\frac{5\sqrt{3}}{4}$ | C. | 4 | D. | $\frac{5\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com