
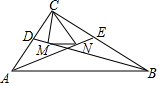
 在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2.
在Rt△ABC中,∠ACB=90°,AE,BD是角平分线,CM⊥BD于M,CN⊥AE于N,若AC=6,BC=8,则MN=2. 分析 延长CM交AB于G,延长CN交AB于H,证明△BMC≌△BMG,得到BG=BC=8,CM=MG,同理得到AH=AC=6,CN=NH,根据三角形中位线定理计算即可.
解答 解:延长CM交AB于G,延长CN交AB于H,
∵∠ACB=90°,AC=6,BC=8,
∴AB=10,
在△BMC和△BMG中,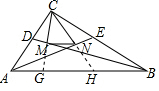
$\left\{\begin{array}{l}{∠MBC=∠MBG}\\{BM=MB}\\{∠BMC=∠BMG}\end{array}\right.$,
∴△BMC≌△BMG,
∴BG=BC=8,CM=MG,
∴AG=2,
同理,AH=AC=6,CN=NH,
∴GH=4,
∴MN=$\frac{1}{2}$GH=2,
故答案为:2.
点评 本题考查的是三角形中位线定理、全等三角形的判定和性质,掌握三角形的中位线平行于第三边,且等于第三边的一半是解题的关键.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:选择题
| A. | 2π cm | B. | 3π cm | C. | 4π cm | D. | 5π cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
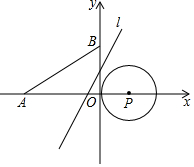 如图,平面直角坐标系中,点P的坐标为(1,0),⊙P的半径为1,点A的坐标为(-3,0),点B在y轴的正半轴上,且OB=$\sqrt{3}$.若直线1:y=$\sqrt{3}$x+m从点B开始沿y轴向下平移,线段AB与线段A′B′关于直线1对称.若线段A′B′与⊙P只有一个公共点,则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$.
如图,平面直角坐标系中,点P的坐标为(1,0),⊙P的半径为1,点A的坐标为(-3,0),点B在y轴的正半轴上,且OB=$\sqrt{3}$.若直线1:y=$\sqrt{3}$x+m从点B开始沿y轴向下平移,线段AB与线段A′B′关于直线1对称.若线段A′B′与⊙P只有一个公共点,则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
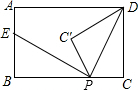 如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:
如图,在矩形ABCD中,AB=3,BC=5,点P是BC边上的一个动点(点P不与点B、C重合),现将△PCD沿直线PD折叠,使点C落在点C’处,作么BPC'的角平分线交AB于点E.设BP=x,BE=y,给出如下结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com