
【题目】如图 ,![]() 是一元二次方程
是一元二次方程![]() 的两个实数根,且
的两个实数根,且![]() ,抛物线
,抛物线![]() 的图象经过
的图象经过![]() .
.

(1)求抛物线的解析式;
(2)设抛物线与![]() 轴的另一个交的为
轴的另一个交的为![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() (2)3
(2)3
【解析】
(1)求出方程的两个实数根,即可得出点A,B的坐标,代入抛物线解析式得出b,c的值即可;
(2)根据抛物线解析式可求出点C、D的坐标,设抛物线的对称轴l与直线BC相交于点M,求出直线BC的解析式,进而得出M的坐标,从而得出三角形的面积.
解:(1)由![]() 解得
解得![]() ,
,![]()
∵![]() ∴
∴![]() ,
,![]() ∴
∴![]() ,
,![]()
则![]() ,解之得
,解之得![]()
因此该抛物线的解析式为![]()
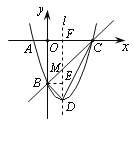
(2)抛物线![]() 的与x轴交点C的坐标为
的与x轴交点C的坐标为
(3,0),顶点D的坐标为(1,-4),抛物线的对称轴l与直线BC相交于点M,
设直线BC的解析式为![]() ,则
,则![]() ,解得
,解得![]()
∴直线BC的解析式为![]() ,
,
∴直线BC与对称轴l的交点M的坐标为(1,-2),∴ MD=2,
∴![]()
∴△BCD的面积为3.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件.经过调查发现,这种商品的销售单价每提高1元,其销售量相应减少20件.设这种商品的销售单提高![]() 元.
元.
(1)现每天的销售量为 件,现每件的利润为 元.
(2)求这种商品的销售单价提高多少元时,才能使每天所获利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,tan∠ACB=2,D在△ABC内部,且AD=CD,∠ADC=90°,连接BD,若△BCD的面积为10,则AD的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】祥云桥位于省城太原南部,该桥塔主体由三根曲线塔柱组合而成,全桥共设13对直线型斜拉索,造型新颖,是“三晋大地”的一种象征.某数学“综合与实践”小组的同学把“测量斜拉索顶端到桥面的距离”作为一项课题活动,他们制订了测量方案,并利用课余时间借助该桥斜拉索完成了实地测量.测量结果如下表.
项目 | 内容 | ||
课题 | 测量斜拉索顶端到桥面的距离 | ||
测量示意图 |
| 说明:两侧最长斜拉索AC,BC相交于点C,分别与桥面交于A,B两点,且点A,B,C在同一竖直平面内. | |
测量数据 | ∠A的度数 | ∠B的度数 | AB的长度 |
38° | 28° | 234米 | |
… | … | ||
(1)请帮助该小组根据上表中的测量数据,求斜拉索顶端点C到AB的距离(参考数据:sin38°≈0.6,cos38°≈0.8,tan38°≈0.8,sin28°≈0.5,cos28°≈0.9,tan28°≈0.5)
(2)该小组要写出一份完整的课题活动报告,除上表的项目外,你认为还需要补充哪些项目(写出一个即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办园博会知识竞赛,打算购买A、B两种奖品.如果购买A奖品10件、B奖品5件,共需120元;如果购买A奖品5件、B奖品10件,共需90元.
(1)A,B两种奖品每件各多少元?
(2)若购买A、B奖品共100件,总费用不超过600元,则A奖品最多购买多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
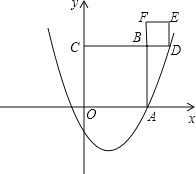
【题目】如图,抛物线![]() 与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则E的坐标是____.
与x轴正半轴交于点A(3,0).以OA为边在x轴上方作正方形OABC,延长CB交抛物线于点D,再以BD为边向上作正方形BDEF.则E的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荆车中学决定在本校学生中,开展足球、篮球、羽毛球、乒乓球四种活动.为了了解学生对这四种活动的喜爱情况,学校随机调查了该校![]() 名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.
名学生,看他们喜爱哪一种活动(每名学生必选一种且只能从这四种活动中选择一种),现将调查的结果绘制成如下不完整的统计图.

(1)![]() _____________,
_____________,![]() _______________;
_______________;
(2)请补全上图中的条形图;
(3)根据抽样调查的结果,请估算全校1800名学生中,大约有多少人喜爱足球;
(4)在抽查的![]() 名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
名学生中,喜爱打乒乓球的有10名同学(其中有4名女生,包括小红、小梅).现将喜爱打乒乓球的同学平均分成两组进行训练,只女生每组分两人.求小红、小梅能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
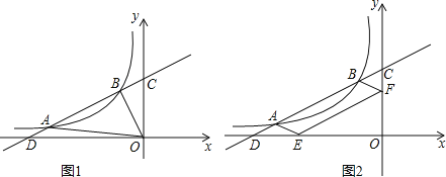
【题目】 如图,一次函数y=0.5x+3的图象与反比例函数y=![]() (k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(k≠0)的图象交于A(-5,a),B两点,与x轴交于点D,与y轴交于点C,且AD=BC.
(1)求此反比例函数的表达式和B点坐标;
(2)连接AO和BO,若点P在x轴上,且S△BDP=![]() S△BOA,求点P的坐标;
S△BOA,求点P的坐标;
(3)如图2,作ABFE,点F和点E分别在y轴和x轴上,求证:∠AED=∠FEO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com