
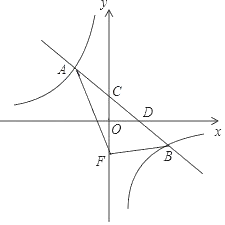
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】《道德经》中的“道生一,一生二,二生三,三生万物”道出了自然数的特征,在数的学习过程中,我们会对其中一些具有某种特性的数进行研究,如学习自然数时,我们研究了奇数、偶数、质数,合数等,现在我们来研究另一种特珠的自然数“纯数”.
定义:对于自然数![]() ,在计算
,在计算![]() 时,各数位都不产生进位,则称这个自然数
时,各数位都不产生进位,则称这个自然数![]() 为“纯数”,例如:32是“纯数”,因为计算
为“纯数”,例如:32是“纯数”,因为计算![]() 时,各数位都不产生进位;23不是“纯数”,因为计算
时,各数位都不产生进位;23不是“纯数”,因为计算![]() 时,个位产生了进位.
时,个位产生了进位.
(1)判断2019和2020是否是“纯数”?请说明理由;
(2)求出不大于100的“纯数”的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级的体育老师为了解本年级学生对球类运动的爱好情况,抽取了该年级部分学生对篮球、足球、排球、乒乓球的爱好情况进行了调查,并将调查结果绘制成如图所示的两幅不完整的统计图[说明:每位学生只选一种自己最喜欢的一种球类)请根据这两幅图形解答下列问题:
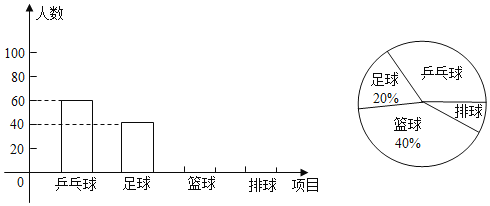
(1)此次被调查的学生总人数为 人.
(2)将条形统计图补充完整,并求出乒乓球在扇形中所占的圆心角的度数;
(3)已知该校有760名学生,请你根据调查结果估计爱好足球和排球的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 同时从点
同时从点![]() 出发,以相同的速度分别沿折线
出发,以相同的速度分别沿折线![]() 、射线
、射线![]() 运动,连接
运动,连接![]() .当点
.当点![]() 到达点
到达点![]() 时,点
时,点![]() 、
、![]() 同时停止运动.设
同时停止运动.设![]() ,
,![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
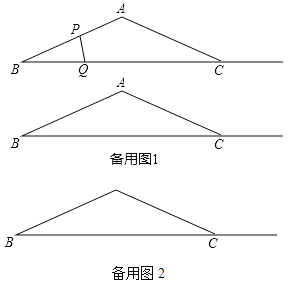
(1)求![]() 长;
长;
(2)求![]() 关于
关于![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)请直接写出![]() 为等腰三角形时
为等腰三角形时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的运算程序中,若开始输入的x值为48,我们发现第一次输出的结果为24,第二次输出输出的结果为12,…则第2014次输出的结果为_____.
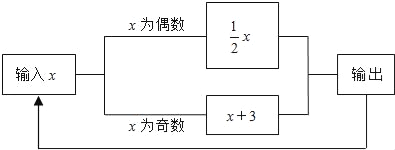
查看答案和解析>>
科目:初中数学 来源: 题型:
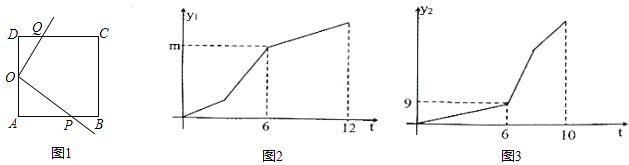
【题目】如图1在正方形![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 从
从![]() 点出发沿
点出发沿![]() 的路线移动到点
的路线移动到点![]() 时停止,出发时以
时停止,出发时以![]() 单位/秒匀速运动:同时点
单位/秒匀速运动:同时点![]() 从
从![]() 出发沿
出发沿![]() 的路线匀速运动,移动到点
的路线匀速运动,移动到点![]() 时停止,出发时以
时停止,出发时以![]() 单位/秒运动,两点相遇后点
单位/秒运动,两点相遇后点![]() 运动速度变为
运动速度变为![]() 单位/秒运动,点
单位/秒运动,点![]() 运动速度变为
运动速度变为![]() 单位/秒运动:图2是射线
单位/秒运动:图2是射线![]() 随
随![]() 点运动在正方形
点运动在正方形![]() 中扫过的图形的面积
中扫过的图形的面积![]() 与时间
与时间![]() 的函数图象,图3是射线
的函数图象,图3是射线![]() 随
随![]() 点运动在正方形
点运动在正方形![]() 中扫过的图形的面积
中扫过的图形的面积![]() 与时间
与时间![]() 的图数图象,
的图数图象,
(1)正方形![]() 的边长是______.
的边长是______.
(2)求![]() ,
,![]() 相遇后
相遇后![]() 在正方形中所夹图形面积
在正方形中所夹图形面积![]() 与时间
与时间![]() 的函数关系式.
的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
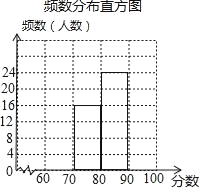
【题目】九 (1)班48名学生参加学校举行的“珍惜生命,远离毒品”知识竞赛初赛,赛后,班长对成绩进行分析,制作如下的频数分布表和频数分布直方图(未完成).余下8名学生成绩尚未统计,这8名学生成绩如下:60,90,63,99,67,99,99,68.
频数分布表
分数段 | 频数(人数) |
60≤x<70 | a |
70≤x<80 | 16 |
80≤x<90 | 24 |
90≤x<100 | b |
请解答下列问题:
(1)完成频数分布表,a= ,b= .
(2)补全频数分布直方图;
(3)全校共有600名学生参加初赛,估计该校成绩90≤x<100范围内的学生有多少人?
(4)九 (1)班甲、乙、丙三位同学的成绩并列第一,现选两人参加决赛,求恰好选中甲、乙两位同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的边OA上有一动点P,从距离O点18cm的点M处出发,沿线段MO,射线OB运动,速度为2cm/s;动点Q从点O出发,沿射线OB运动,速度为1cm/s.P、Q同时出发,设运动时间是t(s).
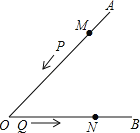
(1)当点P在MO上运动时,PO= cm (用含t的代数式表示);
(2)当点P在MO上运动时,t为何值,能使OP=OQ?
(3)若点Q运动到距离O点16cm的点N处停止,在点Q停止运动前,点P能否追上点Q?如果能,求出t的值;如果不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系xOy中,直线AB与x轴交于点A(-2,0),与反比例函数在第一象限内的图象的交于点B(2,n),连结BO,若S△AOB=4.

(1)求该反比例函数的解析式和直线AB的解析式;
(2)若直线AB与y轴的交点为C,求△OCB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com