
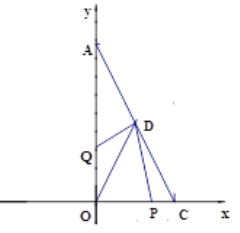
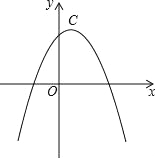
����Ŀ������������12������ͼ����ֱ��������AOC��ֱ�Ƕ���OΪԭ�㣬��OC��OA����ֱ��Ϊx���y�Ὠ��ƽ��ֱ������ϵ����A��0�� a����C��b��0������![]() ��
��
��1����C��������Ϊ__________;A��������Ϊ__________��
��2����֪����������������P��Qͬʱ������P���C�������x�Ḻ������1����λ����ÿ����ٶ������ƶ���Q���O�������2����λ����ÿ����ٶ���y���������ƶ�����Q����A�������˶���֮������AC���е�D����������1,2�������˶�ʱ��Ϊt��t��0�������ʣ��Ƿ����������t��ʹ![]() ,�����ڣ������t��ֵ���������ڣ���˵��������
,�����ڣ������t��ֵ���������ڣ���˵��������
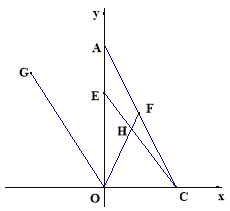
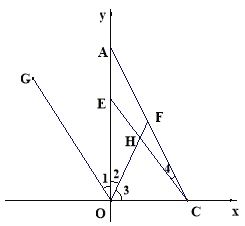
��3����F���߶�AC��һ�㣬������FOC=��FCO, ��G�ǵڶ�������һ�㣬��OG,ʹ����AOG=��AOF����E���߶�OA��һ���㣬��CE��OF�ڵ�H�� ����E���߶�OA���˶��Ĺ����У�![]() ��ֵ�Ƿ�������仯,�����������������ֵ�����仯����˵��������
��ֵ�Ƿ�������仯,�����������������ֵ�����仯����˵��������
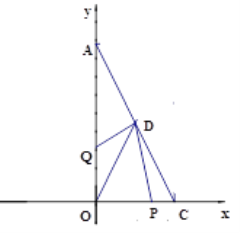
���𰸡���1��A��0,4�� C��2,0������2�����ڣ�t=1����3�����䣬ֵΪ2��
��������
�����������1���ɶ��θ�ʽ�;���ֵ�ķǸ������a,bֵ������֪��A,C�����ꣻ��2��������֪:��Q����A�������˶���֮����,Q���O���˶���A��ʱ��Ϊ2��, �� 0��t��2����Q���߶�AO��,P���߶�OC�ϣ���CP=t ��OC=2�� ��OP=2-t,OQ=2t,��D����������1,2����������ڣ��г���ODP����ODQ�����ȵ�ʽ�ӣ�������������tֵ�Ƿ���ڣ���3��������֪������֤��OG��AC,Ȼ����H����AC��ƽ���߽�OA��M,��OC��N��������ֱ��ƽ���ڴ�����ȣ���������������ʣ��跨����OHCת������1����2����4������OECת������1����4���������������������ı�ֵ��
�����������1���ɶ��θ�ʽ�;���ֵ�ķǸ��Եã�b-2=0,��b=2,a-2b=0,��a-4=0,��a=4����A��0,4�� C��2,0������2��������֪��P���C���˶���O��ʱ��Ϊ2�룬Q���O���˶���A��ʱ��Ϊ2��,��Q����A�������˶���֮��������0<t��2����ʱ��Q���߶�AO��,P���߶�OC�ϣ���CP=t ,OP=2-t,OQ=2t,��D����������1,2������ ![]() ��
��![]() ��
��![]() ����2-t=t����t=1,����������������������t��ʹ
����2-t=t����t=1,����������������������t��ʹ![]() ,��ʱt=1��
,��ʱt=1��
��������֪����֤��OG��AC ����ͼ���ߡ�2����3=90 ����1=��2����3=��FCO���1����2����3����FCO=2����2����3��=180,��OG��AC ,��H����AC��ƽ���߽�OA��M,��OC��N����OG��MN��AC,���GOF=��1����2=��OHN,��NHC=��4������������������ʿɵã���OEC=��OAC����4=��1����4�����OHC=��OHN����NHC=��1����2����4,��![]() ,��
,��![]() ��ֵ��������ֵΪ2��
��ֵ��������ֵΪ2��


 �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д� �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��k��2��x|k|��1��2y=1����k=ʱ�����Ƕ�Ԫһ�η��̣�k=ʱ������һԪһ�η��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������![]() ��
��![]() ��
��![]() ��
��![]() Ϊ���Ѻ������ߡ���
Ϊ���Ѻ������ߡ���
��1����������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����A��������![]() ���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
��3����������![]() �Ķ���ΪC����B������Ϊ����1��4��������
�Ķ���ΪC����B������Ϊ����1��4��������![]() �ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������
�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������![]() �ϣ������������M�����꣬������˵�����ɣ�
�ϣ������������M�����꣬������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺��A��B��CΪ���������㣬����C��A�ľ����ǵ�C��B�ľ���2�������ǾͳƵ�C�ǵ��ǡ�A��B���ĺõ㣮
��1����ͼ1����A��ʾ����Ϊ��1����B��ʾ����Ϊ2����ʾ1�ĵ�C����A�ľ�����2������B�ľ�����1����ô��C�ǡ�A��B���ĺõ㣻 ���磬��ʾ0�ĵ�D����A�ľ�����1������B�ľ�����2����ô��D��A��B���ĺõ㣬����D��B��A���ĺõ㣮�����ں��������ǻ��ǣ�֪ʶ���ã� 
��2����ͼ2��M��NΪ���������㣬��M����ʾ����Ϊ4����N����ʾ����Ϊ��2��������ʾ�ĵ��ǡ�M��N���ĺõ㣻 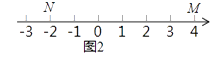
��3����ͼ3��A��BΪ���������㣬��A����ʾ����Ϊ��20����B����ʾ����Ϊ40������һֻ��������P�ӵ�B��������4����λÿ����ٶ������˶��������Aֹͣ����������ʱ��P��A��B��ǡ��һ����Ϊ��������ĺõ㣿 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A����3��2������y��ԳƵĵ������Ϊ��������
A. ��3����2�� B. ��3��2�� C. ����3����2�� D. ��2����3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
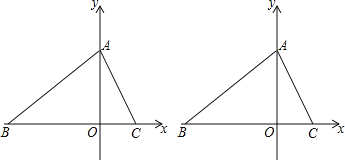
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣮������ABC�ı�BC��ʯ���ϣ���B�������ǣ���5��0������A��y����������ϣ���C��x����������ϣ����ǵ�����ֱ�ΪA��0��m����C��m��1��0������OA��OC��7������P�ӵ�B��������ÿ��2����λ���ٶȣ�������BO�˶������P�˶�ʱ��Ϊt�룮
��1����A��C��������ꣻ
��2������PA����P������BO�����˶�ʱ���Ƿ����ijһʱ�̣�ʹ������POA�������������ABC�����![]() �������ڣ������t��ֵ����д��P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������t��ֵ����д��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���������ͼ��ʾ��һ��������� ![]()
��������������������⣺
��1����С���������Ϊ��4����������Ϊ ��
��2����С���������Ϊ123�������������Ϊ ��
��3��������������г���ʽΪ �� ������Ϊ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com