
 二次函数y=ax2+bx+c(a≠0)的图象如图,请结合图象,解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图,请结合图象,解答下列问题:分析 (1)方程的解就是函数与x轴的交点的横坐标;
(2)不等式ax2+bx+c<0的解集,就是函数在x轴下方部分自变量x的取值范围;
(3)利用待定系数法求解.设出二次函数的三种一般形式求解.
解答 解:(1)方程ax2+bx+c=0的根是x1=-1,x2=3;
(2)出不等式ax2+bx+c<0的解集是x<-1或x>3;
(3)方法一:二次函数的对称轴是x=$\frac{-1+3}{2}$=1,
设二次函数的解析式是y=a(x-1)2+4,
把(-1,0)代入得4a+4=0,
解得a=-1,
则函数的解析式是y=-(x-1)2+4;
方法二:二次函数的顶点坐标是(1,4).
设二次函数的解析式是y=a(x+1)(x-3),
把(1,4)代入得-4a=4,
解得x=-1,
则函数的解析式是y=-(x+1)(x-3);
方法三:二次函数的顶点坐标是(1,4).
设函数的解析式是y=ax2+bx+c,
则$\left\{\begin{array}{l}{a-b+c=0}\\{9a+3b+c=0}\\{a+b+c=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=2}\\{c=3}\end{array}\right.$,
则函数的解析式是y=-x2+2x+3.
在本题中我喜欢的是第一种,在已知顶点的情况下,利用顶点式求解较简单.
点评 本题考查了二次函数图象与函数与x轴的交点之间的关系,以及待定系数法,正确设函数的解析式是关键.


科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
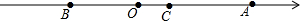 如图,在数轴上原点O表示的数是0,B点表示的数是m,A表示的数是n,且(m+4)2+|n-8|=0.
如图,在数轴上原点O表示的数是0,B点表示的数是m,A表示的数是n,且(m+4)2+|n-8|=0.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
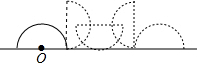 一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)
一个半圆形零件,直径紧贴地面,现需要将零件按如图所示方式,向前作无滑动翻转,使圆心O再次落在地面上止.已知半圆的半径为1m,则圆心O所经过的路线长是πm.(结果用π表示)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 斜边与一条直角边对应成比例的两个直角三角形相似 | |
| B. | 两个等腰直角三角形相似 | |
| C. | 两边对应成比例且有一个角相等的两个三角形相似 | |
| D. | 各有一个角等于100°的两个等腰三角形相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售出件数(件) | 7 | 6 | 3 | 5 | 4 | 5 |
| 每件售价(元) | +3 | +2 | +1 | 0 | -1 | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com