
【题目】一次函数的图象经过点(﹣2,12)和(3,﹣3).
(1)求这个一次函数的表达式.
(2)画出这条直线的图象.
(3)设这条直线与两坐标轴的交点分别为A、B,求△AOB的面积.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t.
⑴用含t的代数式表示:AP= ,AQ= .
⑵当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
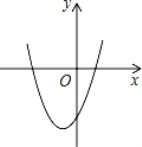
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
x+2与x轴交于点A,B两点,交y轴于C点,抛物线的对称轴与x轴交于H点,分别以OC、OA为边作矩形AECO.
(1)求直线AC的解析式;
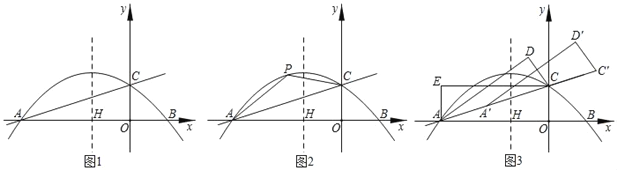
(2)如图2,P为直线AC上方抛物线上的任意一点,在对称轴上有一动点M,当四边形AOCP面积最大时,求|PM﹣OM|的最大值.
(3)如图3,将△AOC沿直线AC翻折得△ACD,再将△ACD沿着直线AC平移得△A'C′D'.使得点A′、C'在直线AC上,是否存在这样的点D′,使得△A′ED′为直角三角形?若存在,请求出点D′的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的有( )
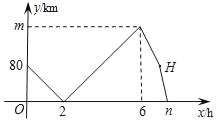
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(11分)如图,四边形ABCD为菱形,点E为对角线AC上的一个动点,连结DE并延长交AB于点F,连结BE.
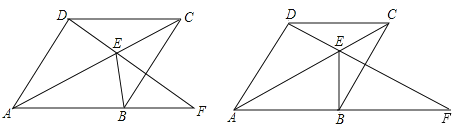
(1)如图①,求证:∠AFD=∠EBC;
(2)如图②,若DE=EC且BE⊥AF,求∠DAB的度数;
(3)若∠DAB=90°且当△BEF为等腰三角形时,求∠EFB的度数(只写出条件与对应的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
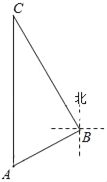
【题目】我国北斗导航装备的不断更新,极大方便人们的出行.光明中学组织学生利用导航到“金牛山”进行研学活动,到达A地时,发现C地恰好在A地正北方向,且距离A地11.46千米.导航显示路线应沿北偏东60°方同走到B地,再沿北偏西37°方向走一段距离才能到达C地,求B,C两地的距离(精确到1千米).
(参考数据sin53°≈0.80,cos53°≈0.60,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com