
 已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).
已知:二次函数y=-x2+bx+c的图象过点A(-1,0)和C(0,2).分析 (1)把A(-1,0)和C(0,2)代入y=-x2+bx+c,根据待定系数法即可求得;
(2)求得翻折部分的解析式,然后令y=0,求得新函数图象G,与x轴的交点,根据图象即可求得.
解答 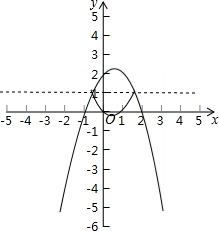 解:(1)把A(-1,0)和C(0,2)代入二次函数解析式得:$\left\{\begin{array}{l}{-1-b+c=0}\\{c=2}\end{array}\right.$,
解:(1)把A(-1,0)和C(0,2)代入二次函数解析式得:$\left\{\begin{array}{l}{-1-b+c=0}\\{c=2}\end{array}\right.$,
解得:b=1,c=2,
则二次函数解析式为y=-x2+x+2;
(2)顶点P($\frac{1}{2}$,$\frac{9}{4}$)翻折后成为N($\frac{1}{2}$,-$\frac{1}{4}$),
∴翻折部分的解析式为y=(x-$\frac{1}{2}$)2-$\frac{1}{4}$,
点M只能位于G的在y轴正半轴部分,
把y=0,代入y=-x2+x+2得-x2+x+2=0,
解得:x=2或x=-1,
把y=0,代入y=(x-$\frac{1}{2}$)2-$\frac{1}{4}$得,(x-$\frac{1}{2}$)2-$\frac{1}{4}$=0,
解得x=1或x=0,
根据图象G,可得m的取值范围为-1≤m≤0或1≤m≤2.
点评 本题考查了待定系数法求二次函数的解析式,二次函数的图象与几何变换,求得翻折后的函数的解析式是解题的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:选择题
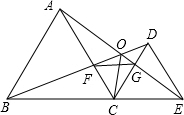 如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④OE=OD+OC.其中正确结论的个数 ( )
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④OE=OD+OC.其中正确结论的个数 ( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AC是⊙O的直径,点B在⊙O上,∠BAC=60°
如图,AC是⊙O的直径,点B在⊙O上,∠BAC=60°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
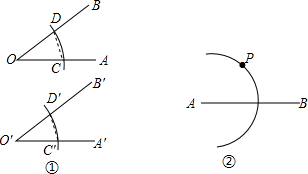 (1)如图①,已知:∠AOB.
(1)如图①,已知:∠AOB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-2)^{2}}$=-2 | B. | -$\sqrt{{3}^{2}}$=3 | C. | $\root{3}{-9}$=-3 | D. | ±$\sqrt{9}$=±3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com