
【题目】完成下列填空.如右图,已知AD⊥BC,EF⊥BC,∠1=∠2. 求证: DG∥BA.

证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFB=∠ADB=90° ( )
∴ ∥ ( )
∴∠1=∠BAD ( )
又∵∠1=∠2 (已知)
∴ (等量代换)
∴DG∥BA. ( )
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,有A(3 , 2) ,B (-1 ,-4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
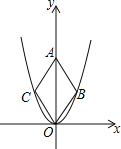
【题目】二次函数y=![]() x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=
x2的图象如图,点O为坐标原点,点A在y轴的正半轴上,点B、C在二次函数y=![]() x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
x2的图象上,四边形OBAC为菱形,且∠OBA=120°,则菱形OBAC的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于被墨水污染,一道几何题仅能见到如图所示的图形和文字:“如图,已知:四边形ABCD中,AD∥BC,∠D=67°,…”
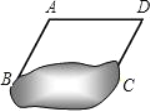
(1)根据以上信息,你可以求出∠A、∠B、∠C中的哪个角?写出求解的过程;
(2)若要求出其它的角,请你添上一个适当的条件: ,并写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明与小华本学期都参加了5次数学考试(总分均为100分),数学老师想判断这两位同学的数学成绩谁更稳定,在作统计分析时,老师需比较这两人5次数学成绩的( )
A. 平均数 B. 方差 C. 众数 D. 中位数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外兴趣小组活动时,老师提出了如下问题:
(1)如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:
延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.

感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形或全等三角形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(2)问题解决:
受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(3)问题拓展:
如图3,在四边形ABDC中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作∠EDF为60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com