
 如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=2CD,点E,F分别为AB,AD的中点,则三角形AEF与多边形BCDFE的面积之比为( )
如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD=2CD,点E,F分别为AB,AD的中点,则三角形AEF与多边形BCDFE的面积之比为( )| A. | 1:7 | B. | 1:6 | C. | 1:5 | D. | 1:4 |
分析 根据三角形的中位线求出EF=$\frac{1}{2}$BD,EF∥BD,推出△AEF∽△ABD,得出 $\frac{{S}_{△AEF}}{{S}_{△ABD}}$=$\frac{1}{4}$,求出 $\frac{{S}_{△CDB}}{{S}_{△ABD}}$=$\frac{\frac{1}{2}•DC•BC}{\frac{1}{2}•AB•BC}$=$\frac{1}{2}$,即可求出△AEF与多边形BCDFE的面积之比.
解答 解:连接BD,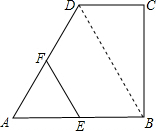
∵F、E分别为AD、AB中点,
∴EF=$\frac{1}{2}$BD,EF∥BD,
∴△AEF∽△ABD,
∴$\frac{{S}_{△AEF}}{{S}_{△ABD}}$=( $\frac{EF}{BD}$)2=$\frac{1}{4}$,
∴△AEF的面积:四边形EFDB的面积=1:3,
∵CD=$\frac{1}{2}$AB,CB⊥DC,AB∥CD,
∴$\frac{{S}_{△CDB}}{{S}_{△ABD}}$=$\frac{\frac{1}{2}•DC•BC}{\frac{1}{2}•AB•BC}$=$\frac{1}{2}$,
∴△AEF与多边形BCDFE的面积之比为1:(3+2)=1:5,
故选C.
点评 本题考查了三角形的面积,三角形的中位线等知识点的应用,主要考查学生运用性质进行推理和计算的能力,题目比较典型,难度适中.


科目:初中数学 来源: 题型:解答题
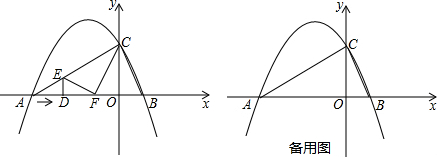
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 参加年级 | A组学生 | 其它组学生 | 总数 |
| 参加人数 | x | 65-x | 65 |
| 每人搬椅子 | 6 | 8 | -- |
| 共搬椅子 | 6x | 8(65-x) | 400 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com