
【题目】已知:如图,斜坡AP的坡度为1:2.4,坡长AP为26米,在坡顶A处的同一水平面上有一座古塔BC,在斜坡底P处测得该塔的塔顶B的仰角为45°,在坡顶A处测得该塔的塔顶B的仰角为76°.求:
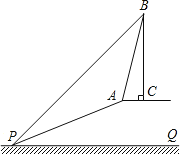
(1)坡顶A到地面PQ的距离;
(2)古塔BC的高度(结果精确到1米).(参考数据:sin76°≈0.97,cos76°≈0.24,tan76°≈4.01)
【答案】(1)10m,(2)古塔BC的高度约为19米.
【解析】试题分析:(1)过点A作AH⊥PQ,垂足为点H,利用斜坡AP的坡度为1:2.4,得出AH,PH,AP的关系求出即可;
(2)利用矩形性质求出设BC=x,则x+10=24+DH,再利用tan76°=![]() ,求出即可.
,求出即可.
试题解析:(1)过点A作AH⊥PQ,垂足为点H.

∵斜坡AP的坡度为1:2.4,
∴![]() ,
,
设AH=5km,则PH=12km,
由勾股定理,得AP=13km.
∴13k=26m. 解得k=2.
∴AH=10m.
答:坡顶A到地面PQ的距离为10m.
(2)延长BC交PQ于点D.
∵BC⊥AC,AC∥PQ,
∴BD⊥PQ.
∴四边形AHDC是矩形,CD=AH=10,AC=DH.
∵∠BPD=45°,
∴PD=BD.
设BC=x,则x+10=24+DH.∴AC=DH=x-14.
在Rt△ABC中,tan76°=![]() ,
,
即![]()
解得x=![]() ,即x≈19,
,即x≈19,
答:古塔BC的高度约为19米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
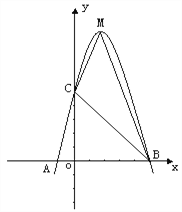
【题目】已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求出对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个足球和3个篮球共需340元,购买5个足球和2个篮球共需410元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据学校的实际情况,需购买足球和篮球共96个,并且总费用不超过5720元.问最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空:
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC.
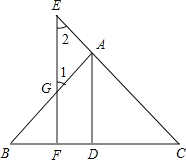
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠ADC=90°,∠EFC=90°(垂线的定义)
∴ =
∥
∴∠1=
∠2=
∵∠1=∠2(已知)
∴ =
∴AD平分∠BAC(角平分线定义)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=30cm.点P从点A出发,以1cm/s的速度向点D移动,点Q从点C出发,以3cm/s的速度向点B运动,点P和点Q分别从点A和点C同时出发,移动时间为ts.规定若其中一个动点先到达端点(终点)时,另一个动点也随之停止运动.
(1)求时间t的取值范围;
(2)当四边形ABQP为矩形时,求时间t的值;
(3)是否存在时间t的值,使得△APQ的面积是△ABC的面积的一半?若存在,请求出t的值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1: ![]() ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: ![]() 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取![]() =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com