
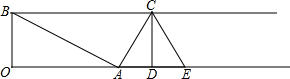
 如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1.
如图,射线BC∥射线OA,BO⊥OA,且OB=2,OA=4,过点A作AC⊥AB交射线BC于C,过点C作CD⊥射线OA交射线OA于D,A,E关于直线CD对称,将△CDE沿射线BC向左向右平移得到△C′D′E′.再将以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形拼成不重叠无缝隙的图形恰好是三角形,请写出所有符合上述条件的BC′的长6或1. 分析 分两种情形①当△CDE向右平移,D′与E重合时,以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形可以拼成不重叠无缝隙的图形恰好是三角形△BHC′,
②当△CDE向右平移,设BE′与C′D′相交于点H,△BHC′与△D′E′H全等时,以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形可以拼成不重叠无缝隙的图形恰好是三角形△AC′D′,分别求出BC′即可解决问题.
解答 解:如图1中,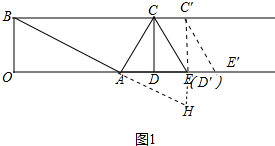
当△CDE向右平移,D′与E重合时,以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形可以拼成不重叠无缝隙的图形恰好是三角形△BHC′,
理由:∵AB⊥AC,
∴∠BAC=90°,
∵BO⊥OA,CD⊥AD,
∴∠O=∠CDA=90°,
∴∠BAO+∠OBA=90°,∠BAO+∠CAD=90°,
∴∠CAD=∠ABO,
∴△ABO∽△CAD,
∴$\frac{AO}{CD}$=$\frac{BO}{AD}$,∠BAO=∠ACD,
∴$\frac{4}{2}$=$\frac{2}{AD}$,
∴AD=DE=1,
∴C′D′=AE=2,∠BAO=∠HAE=∠D′C′E′,
∴以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形可以拼成不重叠无缝隙的图形恰好是三角形△BHC′,
此时BC′=OE=6.
如图2中,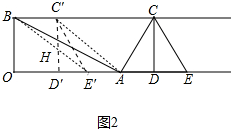
当△CDE向右平移,设BE′与C′D′相交于点H,△BHC′与△D′E′H全等时,以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形可以拼成不重叠无缝隙的图形恰好是三角形△AC′D′,
当BC′=OD′=D′E′=1,∵D′H∥OB,
∴BH=HE′,
∴D′H=$\frac{1}{2}$OB=1=C′H,
∴BC′=C′H=HD′=D′E′,
∴△BC′H,△D′E′H都是等腰直角三角形,
此时△BC′H≌△E′D′H,
∴BC′=1,
综上所述BC′=6或1时,以A,B,C′,E′为顶点的四边形沿着C′D′剪开得到的两个图形可以拼成不重叠无缝隙的图形恰好是三角形.
故答案为6或1.
点评 本题考查图形的拼剪、平移变换、全等三角形的判定和性质等知识,解题的关键是学会分类讨论,需要正确画出图形解决问题,属于中考填空题中的压轴题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
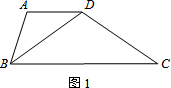 我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.
我们把有一组邻边相等,一组对边平行但不相等的四边形称作“准菱形”.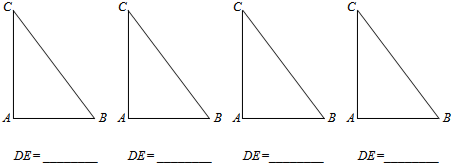
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
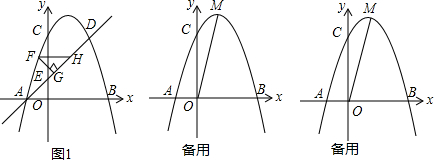
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 姓名 | A | B | C | D | E | F | G | H | I |
| 成绩(米) | 0.91 | 0.95 | 1.10 | 0.98 | 1.08 | 0.96 | 1.12 | 1.18 | 1.17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com