
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

【答案】
见解析;OE=4EF
【解析】试题分析:根据角平分线的性质可得ED=EC,结合OE=OE得出△OED和△OEC全等,从而得出OC=OD,根据等腰三角形三线合一定理得出答案;根据OE平分∠AOB以及∠AOB=60°得到∠AOE=∠BOE=30°,从而得到OE=2DE,根据同理得出DE=2EF,从而得到答案.
试题解析:证明:(1)∵E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA ∴ED=EC ∵OE=OE
∴Rt△OED≌Rt△OEC ∴OC=OD ∵OE平分∠AOB ∴OE是CD的垂直平分线.
(2)OE=4EF
理由如下:∵OE平分∠AOB, ∠AOB=60 ∴∠AOE=∠BOE=30 ∵ED⊥OA ∴OE=2DE
∵∠EFD=90,∠DEO=90-∠DOE=90-30=60 ∴∠EDF=30 ∴DE=2EF ∴OE=4EF


科目:初中数学 来源: 题型:
【题目】把下列各数分别填在相应的横线上:
1,-0.20, ![]() ,325,-789,0,-23.13,0.618,-2014,π,0.1010010001….
,325,-789,0,-23.13,0.618,-2014,π,0.1010010001….
正数有:______________________________________________________;
分数有:______________________________________________________;
负数有:______________________________________________________;
正整数有:____________________________________________________;
非正数有:_____________________________________________________;
负整数有:_____________________________________________________;
非负数有:_____________________________________________________;
负分数有:_____________________________________________________;
非负整数有:___________________________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数的图象的顶点坐标是(2,4),且过另一点(0,﹣4),则这个二次函数的解析式为( )
A. y=﹣2(x+2)2+4 B. y=﹣2(x﹣2)2+4 C. y=2(x+2)2﹣4 D. y=2(x﹣2)2﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
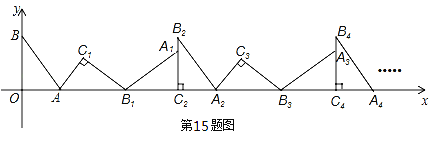
【题目】(2016广东省梅州市第15题)如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用计算器计算数据13.49,13.53,14.07,13.51,13.84,13.98,14.67,14.80,14.61,14.60,14.41,14.31,14.38,14.02,14.17的平均数约为( )
A.14.15
B.14.16
C.14.17
D.14.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com