
【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
![]()
(1)求所捂的多项式;
(2)若x为正整数,任取x的几个值并求出所捂多项式的值,你能发现什么规律?
(3)若所捂多项式的值为144,请直接写出正整数x的值.
【答案】(1)x2-2x+1;(2)所捂多项式的值是代入的正整数x与1的差的平方;(3)13
【解析】
(1)根据题意列出整式相加减的式子,再去括号,合并同类项即可;
(2)令x=1,2,3求出所捂多项式的值,找出规律即可;
(3)根据第(2)问发现的规律可以直接写出x的值.
解:(1)(-2x2+3x-6)-(-3x2+5x-7)
=-2x2+3x-6+3x2-5x+7
=x2-2x+1,
即所捂的多项式是x2-2x+1.
(2)当x=1时,x2-2x+1=1-2+1=0;
当x=2时,x2-2x+1=4-4+1=1;
当x=3时,x2-2x+1=9-6+1=4;
当x=4时,x2-2x+1=16-8+1=9.
规律:所捂多项式的值是代入的正整数x- 1的平方.
(3)若所捂多项式的值为144,
∵144=122,
则正整数x的值是13.


科目:初中数学 来源: 题型:
【题目】某校九年级共有450名学生,随机抽取其中的若干名学生,根据这些学生两次数学模拟考试成绩,分别绘制了如下所示的频数分布直方图,其中图②不完整.

注:① 成绩均为整数;②“60以下”不含60,其余分数段均包含端点;③ 图①、图②分别表示第一次、第二次模拟考试成绩频数分布直方图.
根据以上信息,解答下列问题:
(1)把图②补全;
(2)规定100分以上为优秀,请计算图②中达到优秀的比例;
(3)请你估算九年级学生第二次数学模拟考试达到优秀的人数比第一次数学模拟考试增加多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下文,回答问题:
已知:(1-x)(1+x)=1-x2.
(1-x)(1+x+x2)=_______;
(1-x)(1+x+x2+x3)=_______;
(1)计算上式并填空;
(2)猜想:(1-x)(1+x+x2+…+xn)= ;
(3)你能计算399+398+397…+32+3+1的结果吗?请写出计算过程(结果用含有3幂的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() (
(![]() 为常数).
为常数).
(1)求这个二元一次方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,设
,设![]() ,且m为正整数,求m的值.
,且m为正整数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC
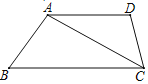
(1)作对角线AC的垂直平分线与边AD、BC分别相交于点E、F(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
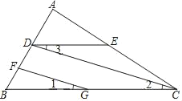
【题目】完成下面的证明
(1)如图,FG∥CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG∥CD(已知)
∴∠2=
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC∥
∴∠B+ =180°
又∵∠B=50°
∴∠BDE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,矩形ABCD的DC边在x轴上,D点坐标为(﹣6,0)边AB、AD的长分别为3、8,E是BC的中点,反比例函数y=![]() 的图象经过点E,与AD边交于点F.
的图象经过点E,与AD边交于点F.
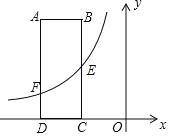
(1)求k的值及经过A、E两点的一次函数的表达式;
(2)若x轴上有一点P,使PE+PF的值最小,试求出点P的坐标;
(3)在(2)的条件下,连接EF、PE、PF,在直线AE上找一点Q,使得S△QEF=S△PEF直接写出符合条件的Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,自变量
的函数,自变量![]() 的取值范围为
的取值范围为![]() ,下表是
,下表是![]() 与
与![]() 的几组对应值
的几组对应值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系中,指出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象.

(2)根据画出的函数图象填空.
①该函数图象与![]() 轴的交点坐标为_____.
轴的交点坐标为_____.
②直接写出该函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
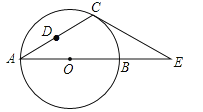
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当![]() CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com