
【题目】如图,大楼外墙有高为AB的广告牌,由距离大楼20米的点C(即CD=20米)观察它的顶部A的仰角是55°,底部B的仰角是42°,求AB的高度.(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43,sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
科目:初中数学 来源: 题型:
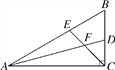
【题目】在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】⑴已知xy=5,x+y=6,则x-y=______
⑵已知(2016-a)(2017-a)=5,(a-2016)2+(2017-a)2的值为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+2与直线l交于点A、B两点,且A点为抛物线与y轴的交点,B(﹣2,﹣4),抛物线的对称轴是直线x=2,过点A作AC⊥AB,交抛物线于点C、x轴于点D.
(1)求此抛物线的解析式;
(2)求点D的坐标;
(3)抛物线上是否存在点K,使得以AC为边的平行四边形ACKL的面积等于△ABC的面积?若存在,请直接写出点K的横坐标;若不存在,请说明理由.[提示:抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣ ![]() ,顶点坐标为(﹣
,顶点坐标为(﹣ ![]() ,
, ![]() )].
)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家到梧州市一茶厂购买茶叶,购买茶叶数量为x千克(x>0),总费用为y元,现有两种购买方式. 方式一:若商家赞助厂家建设费11500元,则所购茶叶价格为130元/千克;(总费用=赞助厂家建设费+购买茶叶费)
方式二:总费用y(元)与购买茶叶数量x(千克)满足下列关系式:y= ![]() .
.
请回答下面问题:
(1)写出购买方式一的y与x的函数关系式;
(2)如果购买茶叶超过150千克,说明选择哪种方式购买更省钱;
(3)甲商家采用方式一购买,乙商家采用方式二购买,两商家共购买茶叶400千克,总费用共计74600元,求乙商家购买茶叶多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
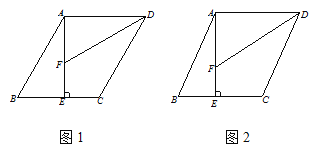
【题目】已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
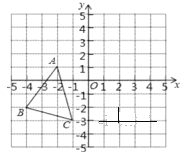
【题目】如图,![]() 中,
中, ![]() ,
,![]() ;
;![]() 是
是![]() 向右平移5个单位向上平移4个单位之后得到的图象
向右平移5个单位向上平移4个单位之后得到的图象
(1)![]() 两点的坐标分别为
两点的坐标分别为![]() ______________
______________![]() ______________.
______________.
(2)作出![]() 平移之后的图形
平移之后的图形![]() .
.
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com