
【题目】学校准备购买A、B两种奖品,奖励成绩优异的同学.已知购买1件A奖品和1件B奖品共需18元;购买30件A奖品和20件B奖品共需480元.
(1)A、B两种奖品的单价分别是多少元?
(2)如果学校购买两种奖品共100件,总费用不超过850元,那么最多可以购买A奖品多少件.
【答案】(1)A奖品的单价为12 元,B奖品的单价为6元;(2)至少购买A奖品41件.
【解析】(1)设A奖品的单价为x 元,B奖品的单价为y元.根据“购买1件A奖品和1件B奖品共需18元;购买30件A奖品和20件B奖品共需480元”,即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)设购买A奖品m件,则购买B奖品(100-m)件.根据总价=单价×购买数量结合总费用不超过850元,即可得出关于m的一元一次不等式,解之取其中最大的整数解即可得出结论.
(1)设A奖品的单价为![]() 元,B奖品的单价为
元,B奖品的单价为![]() 元.由题意得:
元.由题意得:
![]()
解得:![]()
答:A奖品的单价为12 元,B奖品的单价为6元.
(2)设购买A奖品![]() 件,则购买B奖品(100-m)件.由题意得:
件,则购买B奖品(100-m)件.由题意得:
12m+6(100-m)≤850
解得:![]()
∵m为最大正整数,∴![]() 得取值为41.
得取值为41.
答:至少购买A奖品41件.


科目:初中数学 来源: 题型:
【题目】我们在小学已经学过了“对边分别平行的四边形叫做平行四边形”,如图1,平行四边形MNPQ的一边PQ作左右平移,图2反映它的边NP的长度(cm)随时间t(s)变化而变化的情况,请解答下列问题:
(1)在这个变化过程中,自变量是______,因变量是______;
(2)观察图2,PQ向左平移前,边NP的长度是______cm,请你根据图象呈现的规律写出0至5秒间l与t的关系式;
(3)填写下表,并根据表中呈现的规律写出8至14秒间1与t的关系式.
PQ边的运动时间/s | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
NP的长度/cm | 18 | 15 | 12 | ______ | 6 | 3 | 0 |

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]()
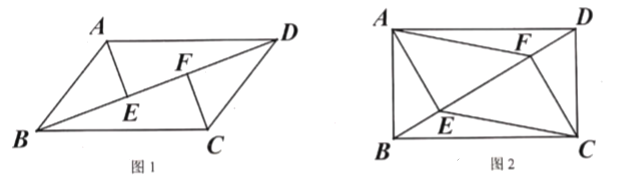
(1)如图1,求证:![]()
(2)如图2,当![]() 时,连接
时,连接![]() 、
、![]() ,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形的面积都等于四边形
,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形的面积都等于四边形![]() 面积的
面积的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空:把下面的推理过程补充完整,并在括号内注明理由,
如图,已知△ABC中,E、F分别是AB、AC上的两点,且EF∥BC,D为EF上一点,且BD=CD,ED=FD,请说明BE=CF.
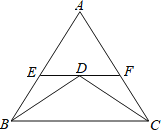
解:∵BD=CD(已知)
∴∠DBC=∠DCB(______)
∵EF∥BC(已知)
∴∠EDB=∠DBC
∠FDC=______(______)
∴∠EDB=∠FDC(等量代换)
在△EBD和△FCD中,
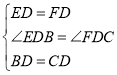
∴△EBD≌△FCD(______)
∴BE=CF(______)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个8×10的网格,每个小正方形的顶点叫格点,每个小正方形的边长均为1,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的图形△![]() .
.
(2)画出△ABC关于点O的中心对称图形 △![]() .
.
(3)△![]() 与△
与△![]() 组成的图形__________ 轴对称图形. (填“是”或“不是”)
组成的图形__________ 轴对称图形. (填“是”或“不是”)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() 经过坐标原点,且当
经过坐标原点,且当![]() 时, y随x的增大而减小.
时, y随x的增大而减小.
(1)求抛物线的解析式;
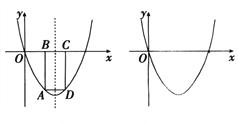
(2)如下图,设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB![]() x轴于点B, DC
x轴于点B, DC![]() x轴于点C.
x轴于点C.
①当 BC=1时,直接写出矩形ABCD的周长;
②设动点A的坐标为(a, b),将矩形ABCD的周长L表示为a的函数,并写出自变量的取值范围,判断周长是否存在最大值,如果存在,求出这个最大值,并求出此时点A的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与双曲线
与双曲线![]()
![]() 交于A点,且点A的横坐标是4.双曲线
交于A点,且点A的横坐标是4.双曲线![]()
![]() 上有一动点C(m,n),
上有一动点C(m,n), ![]() .过点A作
.过点A作![]() 轴垂线,垂足为B,过点C作
轴垂线,垂足为B,过点C作![]() 轴垂线,垂足为D,联结OC.
轴垂线,垂足为D,联结OC.

(1)求![]() 的值;
的值;
(2)设![]() 的重合部分的面积为S,求S与m的函数关系;
的重合部分的面积为S,求S与m的函数关系;
(3)联结AC,当第(2)问中S的值为1时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
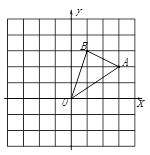
【题目】如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的的坐标分别为A(3,2)、B(1,3).
⑴.请画出将△AOB向左平移3个单位后得到的图形△A1OB1,点B1的坐标为 ;
⑵.请画出将△AOB关于原点O成对称的图形△A2OB2,点A2的坐标为 ;
⑶.在x轴上找一点P,使PA+PB的值最小,则P点的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
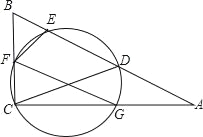
【题目】如图,D为Rt△ABC斜边AB上一点,以CD为直径的圆分别交△ABC三边于E、F、G三点,连接FE,FG.
(1)求证:∠EFG=∠B;
(2)若AC=2BC=4![]() ,D为AE的中点,求FG的长.
,D为AE的中点,求FG的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com