
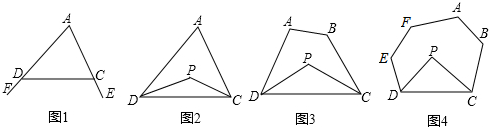
分析 探究一:根据三角形的一个外角等于与它不相邻的两个内角的和可得∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,再根据三角形内角和定理整理即可得解;
探究二:根据角平分线的定义可得∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究三:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究四:根据六边形的内角和公式表示出∠ADC+∠BCD,然后同理探究二解答即可.
解答 解:探究一:∵∠FDC=∠A+∠ACD,∠ECD=∠A+∠ADC,
∴∠FDC+∠ECD=∠A+∠ACD+∠A+∠ADC=180°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠ACD,
=180°-$\frac{1}{2}$(∠ADC+∠ACD),
=180°-$\frac{1}{2}$(180°-∠A),
=90°+$\frac{1}{2}$∠A;
探究三:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠BCD,
=180°-$\frac{1}{2}$(∠ADC+∠BCD),
=180°-$\frac{1}{2}$(360°-∠A-∠B),
=$\frac{1}{2}$(∠A+∠B);
探究四:六边形ABCDEF的内角和为:(6-2)•180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠P=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,
∴∠P=180°-∠PDC-∠PCD,
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠ACD,
=180°-$\frac{1}{2}$(∠ADC+∠ACD),
=180°-$\frac{1}{2}$(720°-∠A-∠B-∠E-∠F),
=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°,
即∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°;
故答案为:∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
点评 本题是三角形综合题目,考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,分别以直角三角形的三边向外作正方形A,B,C.已知SA=64,SB=225,那么正方形C的边长是( )
如图,分别以直角三角形的三边向外作正方形A,B,C.已知SA=64,SB=225,那么正方形C的边长是( )| A. | 15 | B. | 16 | C. | 17 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点(2,0)在x轴上 | B. | 点(0,3)在y轴上 | ||
| C. | (3,-4)与(-4,3)表示两个不同的点 | D. | 点A(1,-2)到y轴的距离为2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两个面积相等的图形是全等图形 | B. | 两个等边三角形一定是全等图形 | ||
| C. | 半径相等的两个圆是全等图形 | D. | 两个含30°角的三角形是全等图形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | MA=MB,NA=NB | |
| B. | MA=MB,MN⊥AB | |
| C. | MA=NA,BM=BN | |
| D. | MA=MB,且点M不在线段AB上,MN平分AB |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2 | B. | y1≤y2 | C. | y1>y2 | D. | y1≥y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(-2,0),B(1,3)设经过A,O两点且顶点C在直线AB上的抛物线为m.
如图,在平面直角坐标系中,已知点A(-2,0),B(1,3)设经过A,O两点且顶点C在直线AB上的抛物线为m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com