
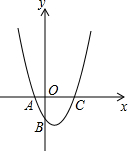
 如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④.
如图示二次函数y=ax2+bx+c的对称轴在y轴的右侧,其图象与x轴交于点A(-1,0)与点C(x2,0),且与y轴交于点B(0,-2),小强得到以下结论:①0<a<2;②-1<b<0;③c=-1;④当|a|=|b|时x2>$\sqrt{5}$-1;以上结论中正确结论的序号为①④. 分析 根据抛物线与y轴交于点B(0,-2),可得c=-2,依此判断③;由抛物线图象与x轴交于点A(-1,0),可得a-b-2=0,依此判断①②;由|a|=|b|可得二次函数y=ax2+bx+c的对称轴为x=$\frac{1}{2}$,可得x2=2,比较大小即可判断④;从而求解.
解答 解:由A(-1,0),B(0,-2),得b=a-2,
∵开口向上,
∴a>0;
∵对称轴在y轴右侧,
∴-$\frac{b}{2a}$>0,
∴-$\frac{a-2}{2a}$>0,
∴a-2<0,
∴a<2;
∴0<a<2;
∴①正确;
∵抛物线与y轴交于点B(0,-2),
∴c=-2,故③错误;
∵抛物线图象与x轴交于点A(-1,0),
∴a-b-2=0,
∵0<a<2,
∴0<b+2<2,
-2<b<0,故②错误;
∵|a|=|b|,二次函数y=ax2+bx+c的对称轴在y轴的右侧,
∴二次函数y=ax2+bx+c的对称轴为x=$\frac{1}{2}$,
∴x2=2>$\sqrt{5}$-1,故④正确.
故答案为:①④.
点评 本题考查了抛物线与x轴的交点,二次函数图象与系数的关系:二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小,当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置,当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右;常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定,△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
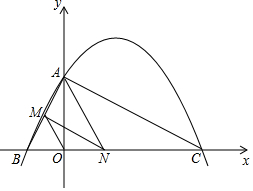 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
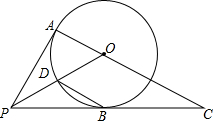 如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
如图,PA,PB是⊙O的切线,A,B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.查看答案和解析>>
科目:初中数学 来源:2016-2017学年山东省新泰市六年级(五四学制)下学期第一次月考数学试卷(解析版) 题型:填空题
如图是一个数值转换机.若输入数3,则输出数是_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com