
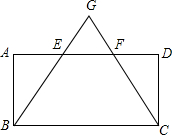
 如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G,GB=GC.
如图,在平行四边形ABCD中,E、F为AD上两点,AE=EF=FD,连接BE、CF并延长,交于点G,GB=GC.分析 (1)根据平行四边形的性质得到AD∥BC,AB=DC,AB∥CD于是得到BE=CF,根据全等三角形的性质得到∠A=∠D,根据平行线的性质得到∠A+∠D=180°,由矩形的判定定理即可得到结论;
(2)①根据相似三角形的性质得到$\frac{{S}_{△GEF}}{{S}_{△GBC}}$=($\frac{EF}{BC}$)2=$\frac{1}{9}$,求得△GBC的面积为18,于是得到四边形BCFE的面积为16;
②根据四边形BCFE的面积为16,列方程得到BC•AB=24,即可得到结论.
解答 (1)证明:∵GB=GC,
∴∠GBC=∠GCB,
在平行四边形ABCD中,
∵AD∥BC,AB=DC,AB∥CD,
∴GB-GE=GC-GF,
∴BE=CF,
在△ABE与△DCF中,
$\left\{\begin{array}{l}{AE=DF}\\{∠AEB=∠DFC}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△DCF,
∴∠A=∠D,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠A=∠D=90°,
∴四边形ABCD是矩形;
(2)①∵EF∥BC,
∴△GFE∽△GBC,
∵EF=$\frac{1}{3}$AD,
∴EF=$\frac{1}{3}$BC,
∴$\frac{{S}_{△GEF}}{{S}_{△GBC}}$=($\frac{EF}{BC}$)2=$\frac{1}{9}$,
∵△GEF的面积为2,
∴△GBC的面积为18,
∴四边形BCFE的面积为16,;
②∵四边形BCFE的面积为16,
∴$\frac{1}{2}$(EF+BC)•AB=$\frac{1}{2}$×$\frac{4}{3}$BC•AB=16,
∴BC•AB=24,
∴四边形ABCD的面积为24,
故答案为:24.
点评 本题考查了相似三角形的判定和性质,矩形的判定和性质,图形面积的计算,全等三角形的判定和性质,证得△GFE∽△GBC是解题的关键.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?
如图所示,港口A位于灯场C的正南方向,港口B位于灯场C的南偏东60°方向,且港口B在港口A的正东方向的90海里处.一艘货轮在上午8时从港口A出发,匀速向港口B航行.当航行到位于灯场C的南偏东30°方向的D处时,接到公司要求提前交货的通知,于是提速到原来速度的1.2倍,于上午12时准时列达港口B,顺利完成交货,求货轮原来的速度是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.78×10-5 | B. | 7.8×10-6 | C. | 7.8×10-7 | D. | 78×10-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
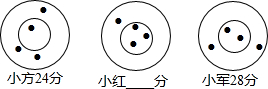 小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )
小方、小红和小军三人玩飞镖游戏,各投四支飞镖,规定在同一圆环内得分相同,中靶和得分情况如图,则小红的得分是( )| A. | 30分 | B. | 32分 | C. | 33分 | D. | 34分 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
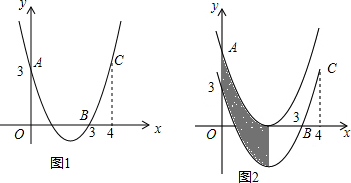
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com