
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)和B(m,0),且3<m<4,则下列说法:①b<0;②a+c=b;③b2>4ac;④2b>3c;⑤![]() =1,正确的是( )
=1,正确的是( )
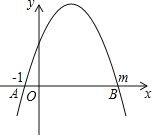
A.①②④B.①③⑤C.②③④D.②③⑤
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图①,在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交线段AB于点N
(1)求证:MN=MC;
(2)若DM:DB=2:5,求证:AN=4BN;
(3)如图②,连接NC交BD于点G.若BG:MG=3:5,求NGCG的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
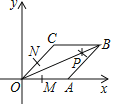
【题目】如图,在平面直角坐标系xOy中,平行四边形OABC的顶点O(0,0),B(3,2),点A在x轴的正半轴上.按以下步骤作图:①以点O为圆心,适当长度为半径作弧分别交边OA、OC于点M、N;②分别以点M、N为圆心,大于![]() MN的长为半径作弧,两弧在∠AOC内交于点P;③作射线OP,恰好过点B,则点A的坐标为( )
MN的长为半径作弧,两弧在∠AOC内交于点P;③作射线OP,恰好过点B,则点A的坐标为( )
A.(![]() ,0)B.(
,0)B.(![]() ,0)C.(
,0)C.( ![]() ,0)D.(2,0)
,0)D.(2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺品店购进A,B两种工艺品,已知这两种工艺品的单价之和为200元,购进2个A种工艺品和3个B种工艺品需花费520元.
(1)求A,B两种工艺品的单价;
(2)该店主欲用9600元用于进货,且最多购进A种工艺品36个,B种工艺品的数量不超过A种工艺品的2倍,则共有几种进货方案?
(3)已知售出一个A种工艺品可获利10元,售出一个B种工艺品可获利18元,该店主决定每售出一个B种工艺品,为希望工程捐款m元,在(2)的条件下,若A,B两种工艺品全部售出后所有方案获利均相同,则m的值是多少?此时店主可获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BC是弦,OD⊥BC于点F,交⊙O于点D,连接AD、CD,∠E=∠ADC.
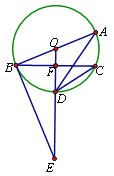
(1)求证:BE是⊙O的切线;
(2)若BC=6,tanA =![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十三五”以来,党中央,国务院不断加大脱贫攻坚的支持决策力度,并出台配套文件,国家机关各部门也出台多项政策文件或实施方案.某单位认真分析被帮扶人各种情况后,建议被帮扶人大力推进特色产业,大量栽种甜橙;同时搭建电商运营服务平台,开设网店销售农产品橙.丰收后,将一批甜橙采取现场销售和网络销售相结合进行试销,统计后发现:同样多的甜橙,现场销售可获利800元,网络销售则可获利1000元,网络销售比现场销售每件多获利5元
(1)现场销售和网络销售每件分别多少元?
(2)根据甜橙试销情况分析,现场销售量a(件)和网络销售量b(件)满足如下关系式:b=﹣![]() a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
a2+12a﹣200.求a为何值时,农户销售甜橙获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最小值是_____.
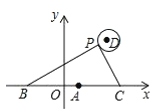
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,点A在y轴的正半轴上,点B在x轴的负半轴上,点C是线段AB上一动点CD⊥y轴于点D,CE⊥x轴于点E,OA=6,AD=OE.
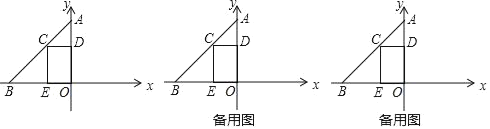
(1)求直线AB的解析式;
(2)连接ED,过点C作CF⊥ED,垂足为F,过点B作x轴的垂线交FC的延长线于点G,求点G的坐标;
(3)在(2)的条件下,连接AG,作四边形AOBG关于y轴的对称图形四边形AONM,连接DN,将线段DN绕点N逆时针旋转90°得到线段PN,H为OD中点,连接MH、PH,四边形MHPN的面积为40,连接FH,求线段FH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个盒子中有1个白球和2个红球,这些球除颜色外都相同.
⑴如果从盒子中随机摸出1个球,摸出红色球的概率为_____________;
⑵若从盒子中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,请通过列表或画树状图的方法,求两次摸到不同颜色球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com